bharath423
- 30
- 0
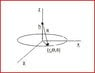
if a point in cylindrical cordinates is A=(r1,\theta1,z1) and another point is
B=(r2,\theta2,z2)
(if ar,a\theta,az are unit vectors)
then the position vector of A is = r1<ar>+\theta1<a\theta>+z1<az>
and the position vector of B is =
r2<ar>+\theta2<a\theta>+z2<az>
so vector BA=
(r1-r2)<ar>+(\theta1-\theta2)<a\theta>+(z1-z2)<az>
am i right upto here??
what is magnitude of vector BA??i think to calculate magnitude we have move back to Cartesian coordinates,am i right??
In cylindrical coordinates at every point we have new unit vectors(i mean in direction) how this is going to be useful for us,than having a fixed unit vectors in Cartesian coordinate system??
why cylindrical coordinates are preferable in case of cylindrical symmetry because even though we use them in order to calculate vectors,distances we have to switch back to Cartesian coordinates??!
i know i totally mis understood the concept but i was not able where i was wrong about cylindrical coordinate system...please some body help me through this..
B=(r2,\theta2,z2)
(if ar,a\theta,az are unit vectors)
then the position vector of A is = r1<ar>+\theta1<a\theta>+z1<az>
and the position vector of B is =
r2<ar>+\theta2<a\theta>+z2<az>
so vector BA=
(r1-r2)<ar>+(\theta1-\theta2)<a\theta>+(z1-z2)<az>
am i right upto here??
what is magnitude of vector BA??i think to calculate magnitude we have move back to Cartesian coordinates,am i right??
In cylindrical coordinates at every point we have new unit vectors(i mean in direction) how this is going to be useful for us,than having a fixed unit vectors in Cartesian coordinate system??
why cylindrical coordinates are preferable in case of cylindrical symmetry because even though we use them in order to calculate vectors,distances we have to switch back to Cartesian coordinates??!
i know i totally mis understood the concept but i was not able where i was wrong about cylindrical coordinate system...please some body help me through this..