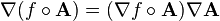Vector calculus chain rule

[daudaudaudau]

Hi. I was looking for a chain rule in vector calculus for taking the gradient of a function such as f(A), where A is a vector and f is a scalar function. I found the following expression on wikipedia, but I don't understand it. It's taking the gradient of f, and applying that to A, and then writing nabla A ?? Can anyone tell me what's going on?

 

[RUber]

Consider $A = [a(x,y,z) \hat x + b(x,y,z) \hat y + c(x,y,z) \hat z ],$ and $f(A) = f(a,b,c),$
then $\nabla f(A) = \hat x \frac{\partial f}{\partial x}\left[\frac{\partial a}{\partial x}+\frac{\partial b}{\partial x}+\frac{\partial c}{\partial x} \right] + \hat y\frac{\partial f}{\partial y}\left[\frac{\partial a}{\partial y}+\frac{\partial b}{\partial y}+\frac{\partial c}{\partial y} \right]+ \hat z \frac{\partial f}{\partial z}\left[\frac{\partial a}{\partial z}+\frac{\partial b}{\partial z}+\frac{\partial c}{\partial z} \right]$
$\nabla f = \hat x \frac{\partial f}{\partial x}+ \hat y \frac{\partial f}{\partial y}+ \hat z \frac{\partial f}{\partial z}$
Also, $\nabla A = \pmatrix{\frac{\partial a}{\partial x} &\frac{\partial b}{\partial x} & \frac{\partial c}{\partial x}\\ \frac{\partial a}{\partial y} &\frac{\partial b}{\partial y} & \frac{\partial c}{\partial y} \\ \frac{\partial a}{\partial z} &\frac{\partial b}{\partial z} & \frac{\partial c}{\partial z}}$
So if you carry out the matrix math and rearrange the terms,

You will see that the equation is true.

 

[daudaudaudau]

Thanks. How would that look in spherical coordinates ?

 

[Fredrik]

I'm just going to answer the first question in a different notation. I like this version of the chain rule: $(f\circ g)_{,i}(x) =f_{,j}(g(x)) g^j{}_{,i}(x)$. Here $_{,i}$ denotes partial differentiation with respect to the $i$th variable, and $g^i$ denotes the real-valued function that takes $x$ to the $i$th component of $g(x)$. I'm using the convention to not write any summation sigmas, since the sum is always over the index that appears twice. For example, if I write $X^i_k Y^k_j$, it means $\sum_{k=1}^n X^i_k Y^k_j$.

Note that the $i$th component of $\nabla(f\circ A)(x)$ is $(f\circ A)_{,i}(x)$.
$$(f\circ A)_{,i}(x)= f_{,j}(A(x))A^j{}_{,i}(x) =\nabla f(A(x))\cdot A_{,i}(x) =(\nabla f\circ A)(x)\cdot A_{,i}(x).$$ I suppose we could also write this as
$$\nabla(f\circ A)(x) =(\nabla f\circ A)(x)\cdot\nabla A(x),$$ but I don't see why we'd want to.