Vector components in the 3 dimensions

[clickcaptain]

Given F = (-20i + 50j = 10k)

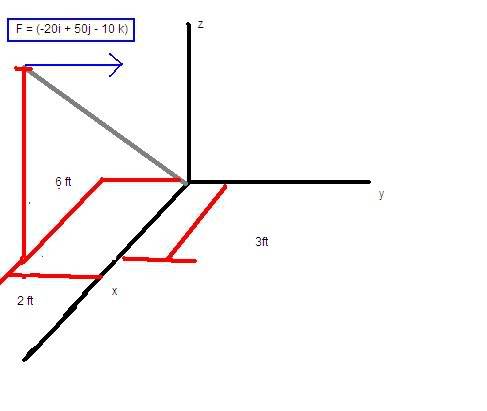
1. The component of the foce projected along the pole AO.
2. The magnitude of the projected component of the F along the pole AO.

I have no idea where to begin, I think I need to find the angles but I'm not sure how in three dimensions.


(please excuse the picture...i know its not the greatest)

 

[tiny-tim]

Welcome to PF!

I think I need to find the angles but I'm not sure how in three dimensions.)

Hi clickcaptain ! Welcome to PF!

No, you don't need to find the angles …

you're thinking of the formula F cosθ for the component of force F in a direction at an angle θ.

But you can also use the formula F.n, the direct product of the force and the unit vector in that direction …

and when the question gives you the coordinates, that's a lot easier!

 

[clickcaptain]

so the unit vector would be ...

position vector of pole = r = 3i - 2j + 6k)
length of r = l = sqrt(3^2 + 2^2 + 6^2) = 7

u = r/l = 3/7i - 2/7 j + 6/7 k

is that right?

then take that times the force vector given?

 

[tiny-tim]

… is that right?

Yup!

(though I would have waited until the next step before dividing by 7 … )

then take that times the force vector given?

(you mean dot, not times, of course )

Yes … that gives you the component of force along that direction.

 

[clickcaptain]

thanks! :-)