Plotting the Poynting vector of a radiating electric dipole [matlab]

[PhDeezNutz]

Homework Statement

This is not so much a homework question but I figured this is the best place to ask for help

According to Jackson (9.18) the $\vec{B}$ and $\vec{E}$ fields of a radiating electric dipole (modulo the time dependence) are

$\vec{B}_{\left( \ell = 1 \right)} = \frac{1}{4\pi} \sqrt{\frac{\mu}{\epsilon}} k^2 \frac{e^{ikr}}{r} \left( 1 - \frac{1}{ikr}\right) \hat{r} \times \vec{p}$

and

$\vec{E}_{\left(\ell =1 \right)} = \frac{1}{4 \pi \epsilon} \left[ k^2 \left( \hat{r} \times \vec{p} \right) \times \hat{r} \frac{e^{ikr}}{r} + \left[ 3 \left(\hat{r} \cdot \vec{p} \right) \hat{r} - \vec{p}\right] \left( \frac{1}{r^3} - \frac{ik}{r^2}\right)e^{ikr}\right]$

I'd like to plot a snapshot of Poynting vector field at time $t=0$ and then eventually string together an animation with a for loop. Something like the following albeit in 3 dimensions instead of two

https://upload.wikimedia.org/wikipedia/commons/2/2e/DipoleRadiation.gif

Relevant Equations

Taking the fields above and breaking them apart by spherical basis components I get

$\vec{B_{(\ell = 1)}} = \frac{1}{4 \pi } \sqrt{\frac{\mu}{\epsilon}} e^{ikr} \left( \frac{k^2r^2 + ikr}{r^3}\right) p_\theta \hat{\phi} - \frac{1}{4 \pi } \sqrt{\frac{\mu}{\epsilon}} e^{ikr} \left( \frac{k^2r^2 + ikr}{r^3}\right) p_\phi \hat{\theta}$

and

$\vec{E}_{\ell =1} = \frac{1}{2 \pi \epsilon} \left(\frac{e^ikr}{r^3} \right) \left( - i kr +1\right) p_r \hat{r} + \frac{1}{4 \pi \epsilon} \left( \frac{e^{ikr}}{r^3} \right) \left( k^2r^2 + ikr -1 \right) p_\theta \hat{\theta} + \frac{1}{4 \pi \epsilon} \left( \frac{e^{ikr}}{r^3} \right) \left( k^2r^2 + ikr -1 \right) p_\phi \hat{\phi}$

Also from what I understand when dealing with complex valued vectors the Poynting Vector is defined as

$\vec{S} = \frac{1}{2}Re\left(\vec{E} \times \vec{H}^{*} \right) = \frac{\mu}{2}\left( \vec{E} \times \vec{B}^{*}\right)$

For some strange reason the spherical basis convention in matlab is different from the physics convention so $\vec{B}$ and $\vec{E}$ in the matlab convention

[img]https://www.mathworks.com/help/phased/ref/spherical_basis.png[\img]

$\vec{B} = -\frac{1}{4 \pi } \sqrt{\frac{\mu}{\epsilon}} e^{ikr} \left( \frac{k^2r^2 + ikr}{r^3}\right) p_{el} \hat{az} + \frac{1}{4 \pi } \sqrt{\frac{\mu}{\epsilon}} e^{ikr} \left( \frac{k^2r^2 + ikr}{r^3}\right) p_{az} \hat{el}$

$\vec{E} = \frac{1}{4 \pi \epsilon} \left( \frac{e^{ikr}}{r^3} \right) \left( k^2r^2 + ikr -1 \right) p_{az}\hat{az} + \frac{1}{4 \pi \epsilon} \left( \frac{e^{ikr}}{r^3} \right) \left( k^2r^2 + ikr -1 \right) p_{el}\hat{el} + \frac{1}{2 \pi \epsilon} \left(\frac{e^ikr}{r^3} \right) \left( - i kr +1\right) p_r \hat{r}$

Since this is in the long wave length limit we have to appropriately choose the wave number and magnitude of the dipole moment. I will show my reasoning for "the scales" later.

I've attached a .txt file of my script for those who want to take a look at it

Here's a picture of my vector field at time t = 0

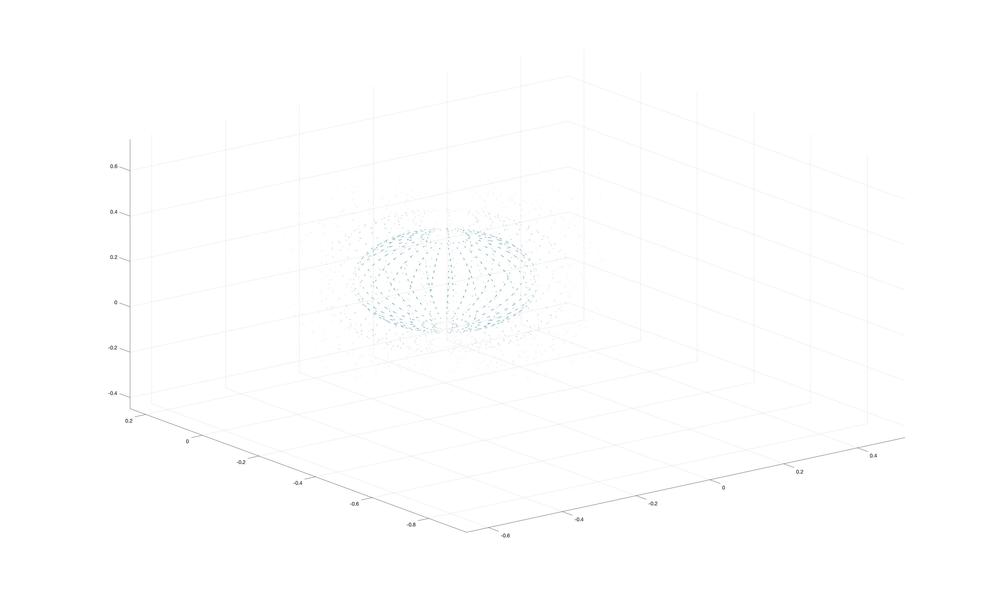
I'm very concerned about this picture because from my understanding the Poynting vector is supposed to point outwards and not loop back around, this looks nothing like the Poynting Vector field in the wikipedia .gif and I'm almost certain that I converted Jackson's formulas correctly.

The only thing I can think of is that my range of my grid is only in the "near/static zone" where maybe the Poynting Vectors do loop back around. The problem is when I expand my range the vector field is so "sparse" that it's hard to discern any salient features.

I think my problem is a problem of scale.

And since we are talking about scale I think I should qualify some of my choices for values of $k$ and $p$ as well as the range.

In the long wavelength limit $\lambda \gg d \Rightarrow \frac{2 \pi}{k} \gg d$ where $d$ is the dimension of the charge distribution creating the dipole. $k \ll \frac{2 \pi}{d}$Starting off with arbitrary values

n = 25;
rmin = 0.2;
rmax = 2.0;
phi = linspace(-pi,pi - ((n)^(-1))*2*pi,n);
theta = linspace(-0.5*pi,0.5*pi - ((n)^(-1))*2*pi,n);
r = linspace(rmin,rmax,n);

Notice I have filtered out the origin by creating a sphere around it with diameter 0.4. To me that means I have implicitly assumed $d = 0.4$. That means $k \ll 5 \pi$. To me "much much less than" means 3 orders or magnitude so $k = \frac{5 \pi}{1000}$

I chose p according to

p = 0.001*(r(n-1)-r(n-2));
p = [0;0;p];

My reasoning is that we want a dipole moment that is small compared to the spatial steps of r, that way we get more variations over a small area and therefore can discern more salient features.

Again, I think my problem is a problem of scale that I don't know how to fix. I want to find a way to capture the salient features of the near, intermediate, and radiation zone without expanding my view so much that the vectors are so small that they disappear.....perhaps I should expand the spatial range and normalize my vectors? I'm going to try that...but I'm going to leave this thread up incase someone is able to make suggestions that I haven't even thought about/correct my work both computationally and conceptually. I'm pretty sure my component wise calculation of Jackson's formulas are right so maybe I messed up in converting to the MATLAB convention?

Every bit of help is appreciated.

In case people have apprehensions about downloading a .txt file I'll just copy and paste my entire script in the next post.

 

[PhDeezNutz]

o ahead and define constants we'll need and the dipole moment
const1 = ((4*pi)^(-1))*sqrt((4*pi*(10)^(-7))*(8.85*(10)^(-12))^(-1));
const2 = ((2*pi)^(-1));
const3 = 0.5*const2;
mu = 4*pi*((10)^(-7));
const4 = 180 * ((pi)^(-1));
epsilon = 8.85*((10)^(-12));
kwave = 0.001*5*pi;
const5 = (4*pi*epsilon)^(-1);

%2) Form spherical meshgrid, avoid redundancies and singularities

n = 25;
rmin = 0.2;
rmax = 2.0;
phi = linspace(-pi,pi - ((n)^(-1))*2*pi,n);
theta = linspace(-0.5*pi,0.5*pi - ((n)^(-1))*2*pi,n);
r = linspace(rmin,rmax,n);
p = 0.001*(r(n-1)-r(n-2));
p = [0;0;p];
%3) Create a meshgrid of sherical coordinates, extract vectors, and transpose[Phi,Theta,R] = meshgrid(phi,theta,r);
SphericalPointsfromMesh = [Phi(:),Theta(:),R(:)];
SphericalPointsfromMeshT = SphericalPointsfromMesh';

%4) Create a repeated matrix of p

PmatC = repmat(p,[1 size(SphericalPointsfromMeshT,2)]);

%5) We want to convert PmatC to spherical points at each point given in SphericalPointsfromMeshT

%5-1) In order to do that we need to convert SphericalPointsfromMeshT to degrees

SphericalPointsfromMeshD = [const4*Phi(:),const4*Theta(:),R(:)];
SphericalPointsfromMeshDT = SphericalPointsfromMeshD';
azdegrees = SphericalPointsfromMeshDT(1,:);
eldegrees = SphericalPointsfromMeshDT(2,:);%5-2) I think we're ready to do what we set out to do in (5)

for i1 = 1:size(SphericalPointsfromMeshDT,2)
PmatS(:,i1) = cart2sphvec(p,azdegrees(1,i1),eldegrees(1,i1));
end

%6) Now to create the B components in spherical basis

for i2 = 1:size(SphericalPointsfromMeshDT,2)
Baz(1,i2) = - const1 * exp(1i*kwave*SphericalPointsfromMeshDT(3,i2))*(SphericalPointsfromMeshDT(3,i2)^(-3))*((kwave^2)*((SphericalPointsfromMeshDT(3,i2)^(2)) + 1i*kwave*SphericalPointsfromMeshDT(3,i2))*(PmatS(2,i2)));
end

for i3 = 1:size(SphericalPointsfromMeshDT,2)
Bel(1,i3) = const1 * exp(1i*kwave*SphericalPointsfromMeshDT(3,i3))*(SphericalPointsfromMeshDT(3,i3)^(-3))*((kwave^2)*((SphericalPointsfromMeshDT(3,i3)^(2)) + 1i*kwave*SphericalPointsfromMeshDT(3,i3))*(PmatS(1,i3)));
end

Bsr = zeros(size(Bel));

% Vertically concatenate

Bs = vertcat(Baz,Bel,Bsr);

% Convert Bs back to cartesian (at least try to)

for i4 = 1:size(Bs,2)
BC(:,i4) = sph2cartvec(Bs(:,i4),azdegrees(1,i4),eldegrees(1,i4));
end% Now to create E

for i5 = 1:size(SphericalPointsfromMeshDT,2)
Eaz(1,i5) = const5*exp(1i*kwave*SphericalPointsfromMeshDT(3,i5))*(SphericalPointsfromMeshDT(3,i5)^(-3))*((kwave^2)*((SphericalPointsfromMeshDT(3,i5)^(2)) + 1i*kwave*SphericalPointsfromMeshDT(3,i5) -1))*(PmatS(1,i5));
end

for i6 = size(SphericalPointsfromMeshDT,2)
Eel(1,i6) = const5*exp(1i*kwave*SphericalPointsfromMeshDT(3,i6))*(SphericalPointsfromMeshDT(3,i6)^(-3))*((kwave^2)*((SphericalPointsfromMeshDT(3,i6)^(2)) + 1i*kwave*SphericalPointsfromMeshDT(3,i6) -1))*(PmatS(2,i6));
end

for i7 = 1:size(SphericalPointsfromMeshDT,2)
Er(1,i7) = 0.5*const1*exp(1i*kwave*SphericalPointsfromMeshDT(3,i7))*(SphericalPointsfromMeshDT(3,i7)^(-3))*(-1i*kwave*SphericalPointsfromMeshDT(3,i7) + 1)*(PmatS(3,i7));
end

% Vertically concatenate

Es = vertcat(Eaz,Eel,Er);

% Convert Es back to Cartesian (at least try to)

for i8 = 1:size(Es,2)
EC(:,i8) = sph2cartvec(Es(:,i8),azdegrees(1,i8),eldegrees(1,i8));
end

% Now calculate the Poynting Vector

H = ((mu)^(-1))*BC;
Hconj = conj(H);

EcrossHconj = cross(EC,Hconj);

Realpart = real(EcrossHconj);

FinalPoyntingVector = 0.5*Realpart;

% Now to plot the vector field and hopefully get something that is not ridiculous

%first have to convert the entire position grid to cartesian

[X,Y,Z] = sph2cart(Phi,Theta,R);

CartesianPointsfromMesh = [X(:),Y(:),Z(:)];

CartesianPointsfromMeshT = CartesianPointsfromMesh';

% Now to hopefully plot the vector field and not get something ridiculous

quiver3(CartesianPointsfromMeshT(1,:),CartesianPointsfromMeshT(2,:),CartesianPointsfromMeshT(3,:),FinalPoyntingVector(1,:),FinalPoyntingVector(2,:),FinalPoyntingVector(3,;))

 

[PhDeezNutz]

Alright I tried something new but I didn't have much luck

First I tried expanding my grid so that it would encompass "the far/radiation zone"

according to Jackson this means $kr \gg 1 \Rightarrow r \gg \frac{1}{k} = \frac{1}{(0.001)(5 \pi)}$ so I made rmax = 10^6

In theory that should encompass the radiation zone.

I also suspected that a lot of my vectors were too faint to show up because their magnitudes were really small so I normalized them.

for i9 = 1:size(FinalPoyntingVector,2)
NormFinalPoyntingVector(1,i9) = sqrt((FinalPoyntingVector(1,i9)).^2 + (FinalPoyntingVector(2,i9)).^2 + (FinalPoyntingVector(3,i9)).^2);
end

NFPVnegative1 = NormFinalPoyntingVector.^(-1);

% Try plotting vector field this time normalized

figure

quiver3(CartesianPointsfromMeshT(1,:),CartesianPointsfromMeshT(2,:),CartesianPointsfromMeshT(3,:),NFPVnegative1.*FinalPoyntingVector(1,:),NFPVnegative1.*FinalPoyntingVector(2,:),NFPVnegative1.*FinalPoyntingVector(3,;

My results were not satisfactory, I'm still getting Poynting vectors circulating around the origin of the dipole instead of radiating outwards even when I expand the range to supposedly encompass the far radiation zone

I'm guessing that this formula is wrong$\vec{S} = \frac{1}{2}Re\left(\vec{E} \times \vec{H}^{*} \right) = \frac{\mu}{2}Re\left( \vec{E} \times \vec{B}^{*}\right)$

If so what is the correct formula?

What I do find sort of comforting is that my vector field is "exactly the opposite" of what I want. If only my field was orthogonal to the one I have I'd be in a good position.

 

[TSny]

I'm guessing that this formula is wrong

$\vec{S} = \frac{1}{2}Re\left(\vec{E} \times \vec{H}^{*} \right) = \frac{\mu}{2}Re\left( \vec{E} \times \vec{B}^{*}\right)$

If so what is the correct formula?

This expression gives the time average of the Poynting vector. It is time-independent due to the factor $e^{+i\omega t}$ in $\vec B^*$ canceling with the factor $e^{-i\omega t}$ in $\vec E$. See here.
Jackson (3rd ed.) has some discussion in section 6.9.

If you want the instantaneous Poynting vector, use

$\vec{S} = Re\left(\vec{E}\right)\times Re\left(\vec{H} \right)$

I won't be of much help with the computer plotting. The magnitude of the E and B fields vary rapidly with distance from the dipole when you are in the near-field region. So, scaling the Poynting vector to get a nice plot might be tricky.

The field pattern is rotationally invariant for rotations around the axis of the dipole. So, I don't see the need to do a 3D plot.

 

[PhDeezNutz]

This expression gives the time average of the Poynting vector. It is time-independent due to the factor $e^{+i\omega t}$ in $\vec B^*$ canceling with the factor $e^{-i\omega t}$ in $\vec E$. See here.
Jackson (3rd ed.) has some discussion in section 6.9.

If you want the instantaneous Poynting vector, use

$\vec{S} = Re\left(\vec{E}\right)\times Re\left(\vec{H} \right)$

I won't be of much help with the computer plotting. The magnitude of the E and B fields vary rapidly with distance from the dipole when you are in the near-field region. So, scaling the Poynting vector to get a nice plot might be tricky.

The field pattern is rotationally invariant for rotations around the axis of the dipole. So, I don't see the need to do a 3D plot.

I will try Re{E} x Re{H} and see what happens. Given that I plotted the time averaged Poynting vector do you find anything wrong with the fact that it’s not pointing outwards?

Also thank you!

edit: I’m doing it in 3D because I eventually want to try and plot the radiating quadrupole.

 

[TSny]

I will try Re{E} x Re{H} and see what happens. Given that I plotted the time averaged Poynting vector do you find anything wrong with the fact that it’s not pointing outwards?

The time-averaged S should point radially outward in the $\hat r$ direction even in the near field region.

The instantaneous S in the near field (where r is less than roughly a wavelength) can have a negative radial component at certain times at certain points. But, for r greater than a few wavelengths, you should find that S points nearly radial at all times. In the far-field region, where r is much greater than a wavelength, only the radial component of S is significant.

edit: I’m doing it in 3D because I eventually want to try and plot the radiating quadrupole.

Ah. That would be very interesting to see

 

[PhDeezNutz]

Well then there’s something wrong with my code then so I’ll have to go back to the drawing board. I have other things I need to attend to but I should be able to get back to it soon enough.

 

[PhDeezNutz]

I tried $Re(\vec{E}) X Re(\vec{H})$ at $t = 0$ and got the following

Some comments:

1) The"lack of coverage" is concerning. There seems to be a substantial part of the field missing, maybe when I create an animation the missing parts will fill in?

2) My dipole moment was defined to be in the z-direction and to me my picture is "off by 90 degrees"; for some reason I feel like the Poynting vectors should be coming out of the sides of the dipole instead of out of the top.

As a side note when I look at the top view of my field I get something really beautiful (yet maybe useless and wrong)

Edit: furthermore the formulas I used from Jackson are supposed to encompass both the near and far zones...I'm not seeing characteristic near zone features.

 

[TSny]

Yes, that doesn't look right. You might try a 2D plot, such as the $\phi = 0$ plane. Your expressions for the fields in your first post look correct to me (with MatLab's "elevation" angle $\theta$).

I used Mathematica to make some plots of the S-field at one instant of time (t = 0). I certainly could have made some errors in deriving the expressions for the components of S. But, these plots might give you something to compare with. I scaled the vectors in such a way that a 10-fold change in the magnitude of S changes the size of the plotted vectors by only a factor of $10^{1/5}$. This allows for an exploration of the near field region without huge changes in the size of the vectors.

I chose $k = 2\pi$ so that the wavelength of the radiation is 1 unit. This makes the S-field have a "wavelength" of 0.5 unit.

Here is the S-field that I got for one instant of time in a region very near the dipole (out to only 0.1wavelength). I blocked out a region less than 0.02 wavelength from the dipole in order to avoid extremely large field values.

Here is a region out to about 1.5 wavelengths

Here is a patch of area .5 < x < 2 and .5 < y < 2

Here is a patch of "far field" where 20<x<22 and 20<y<22

 

[TSny]

I don't understand your choice of the value of $k$ which makes the wavelength of the radiation equal to 400 units of distance. I believe you let $r_{max} = 2$ in your code. So, that would mean you are plotting in the extreme near field.

 

[PhDeezNutz]

I don't understand your choice of the value of $k$ which makes the wavelength of the radiation equal to 400 units of distance. I believe you let $r_{max} = 2$ in your code. So, that would mean you are plotting in the extreme near field.

I actually kept the value of $k$ and $p$ the same while making $r_{min }= 0.4$ along with changing $r_{max } = 10^{10}$

and I still don't get what I want.

Notice that I rotated the figure to give a head on view of the $xz-plane$ i.e. ($\phi = 0$).
I'm clearly doing something wrong because I've expanded the scale well beyond a few wavelengths and I'm still not getting purely radial components.

Edit: I normalized the $\vec{S}$ vectors so that they would all show up.

Commentary: My field is almost the exact opposite of what I want; I have radial fields up close and angular fields out far...I want angular fields up close and radial fields far away.

Edit2: I feel like my field would be perfect if it was just perpendicular to the one I have.

 

[TSny]

The value of $p$ doesn't matter. It just enters as part of the overall constant for S.

I'm not familiar with MatLab, so I can't help much there. I noticed you use several functions that appear to convert between spherical coordinates and cartesian coordinates, such as

sph2cart
sphcartvec
cart2sphvec
vertcat

If I were you, I would write a short program to test all of these with specific numerical examples to make sure they are giving you what you think they should. There's also the headache of dealing with MatLabs elevation angle versus the usual spherical coordinate angle $\theta$.

I noticed you have a command:
PmatS(:,i1) = cart2sphvec(p,azdegrees(1,i1),eldegrees(1,i1));

I would think that cart2sphvec would convert from cartesian to spherical. But it looks like you are inputting spherical coordinates here. But, as I said, I'm not familiar with these functions.

 

[PhDeezNutz]

@TSny may I ask what expressions for the components of the $\vec{E}$,$\vec{B}$, and $\vec{S}$ fields are? (In cartesian or spherical)

I'm pretty sure the expressions in the first post are wrong; I believe the mistake I made was when I took the curl of $\vec{B}$ to find $\vec{E}$ (modulo the time dependency) is treating the components of $\vec{p}$ as constants.

I'm fairly certain that I know what those functions are doing as I wrote a program with them to plot the field of a static electric dipole and it turned out exactly as I wanted.

sph2cart transforms spherical to cartesian and accepts radian arguments

sph2cartvec transforms a vector in spherical ($\hat{az}$),$\hat{el}$,$\hat{r}$) to cartesian at a given azimuth and elevation angle (in degrees)

cart2sphvec transforms a vector in cartesian basis to spherical basis at a given azimuth and elevation angle.

vertcat vertically concatenates row vectors

Another thing I need to consider is "retarded time".

Also, I tried multiplying by

$e^{-i \left(\omega}t -i\frac{\omega R}{c}}$ to no avail. My (probably flawed) reasoning is this. I changed around my formulas and got a purely radial field for S for $t=0$

I find it comforting that there is no radiation along the axis of the dipole but I'm still not getting near field behavior

 

[PhDeezNutz]

@TSny I think I got it

I changed my scale to a few wavelengths and I got near field behavior.

Notice that at certain radial distances the Poynting vectors point in the polar direction and in between those "rings" it points radially.

Here's a better picture.

You weren't joking when you said something to the effect of "capturing near field and far field behavior in the same plot might be difficult"

Thank you very much for all your help. I will update this thread when I have an animation that contains contour plots.

Now I have to get back to all my other homework that I haven't done :D

 

[TSny]

@TSny may I ask what expressions for the components of the $\vec{E}$,$\vec{B}$, and $\vec{S}$ fields are? (In cartesian or spherical)

I only considered the case where $\vec p$ is along the z-axis. For convenience, let $\Phi \equiv kr-\omega t$.

In spherical coordinates I get (in Gaussian units)
$$E_r = \frac{2pk}{r^2}\cos \theta \left[ \sin\Phi+\frac{1}{kr}\cos\Phi\right]$$
$$E_\theta = -\frac{pk^2}{r}\sin \theta \left[ \left( 1-\frac{1}{(kr)^2} \right) \cos\Phi-\frac{1}{kr}\sin\Phi\right]$$
$$B_\phi = -\frac{pk^2}{r}\sin \theta \left[ \cos\Phi-\frac{1}{kr}\sin\Phi\right]$$

For the components of the Poynting vector I get

$$
S_r = \frac{cp^2k^4}{8 \pi r^2}\sin^2\theta \left[ 1+\left(1-\frac{2}{(kr)^2}\right)\cos(2 \Phi) - \left(\frac{2}{kr}-\frac{1}{(kr)^3}\right)\sin(2 \Phi)\right] $$
$$S_\theta = \frac{cp^2k^3}{4 \pi r^3}\sin\theta \cos\theta \left[ \left(1-\frac{1}{(kr)^2}\right)\sin(2 \Phi)+ \frac{2}{kr}\cos(2 \Phi)\right]
$$

I hope I typed this correctly.

 

[PhDeezNutz]

@TSny

I believe I messed up majorly

I created a contour plot in the xz-plane of the poynting vector of a radiating dipole (oscillating in the z-direction) and got something supper messed up.

To me this looks like more like a quadrupole than a dipole. How bad did I mess up?

 

[TSny]

Are you plotting contours of the magnitude of S? You plotted out to 600 units. How many wavelengths is this?

Here's what I get at t = 0 for a distance out to 3 wavelengths from the dipole with the central-region blocked out within 1/2 wavelength. I had to do some scaling to get a decent graph.

Here's closer to the dipole out to a distance of 1 wavelength with blocking within 0.1 wavelength

 

[PhDeezNutz]

Are you plotting contours of the magnitude of S? You plotted out to 600 units. How many wavelengths is this?

Here's what I get at t = 0 for a distance out to 3 wavelengths from the dipole with the central-region blocked out within 1/2 wavelength. I had to do some scaling to get a decent graph.

View attachment 256921Here's closer to the dipole out to a distance of 1 wavelength with blocking within 0.1 wavelength
View attachment 256922

Yes I am plotting the magnitude of S.

600 is 1.5 wavelengths.since $k = (0.001)(5)\pi$

and $k = \frac(2 \pi}{\lambda}$

When I expand it to 2400 (6 wavelengths) and increased the number of spatial divisions by a factor of 2.

If anything I would think that that the contours would be "circling back to the origin".

Edit: It really feels like I inadvertently solved the quadrupole term of the magnetic vector potential.

 

[PhDeezNutz]

@TSny

Not as nice as yours but I think I got it. I made some algebraic mistakes trying to break apart Jackson's expressions component wise and now I have fixed them.

Any idea why past a certain range it just all becomes one color? I would like more "waves that don't circle back to the origin" in my pic

Side commentary: Also apparently when I change the number of spatial divisions my code falls apart because array dimensions don't agree...Weird I thought my code was more robust than that. I'll have to take a look at it.

Edit: Does mathematica inherently allow you to plot vector fields in spherical coordinates without having to convert to cartesian first? Furthermore does it allow you to construct contours in spherical coordinates? From what I understand MATLAB requires cartesian meshgrid construction from the beginning in order to construct contours because MATLAB cannot interpolate in spherical (because step size and direction are unclear?).

If the answer is yes to any of these questions then I might have to consider switching to mathematica.

 

[PhDeezNutz]

Got more waves that don't circle back to the origin when I increased the number of levels in my contour plot from 10 to 100.

 

[TSny]

Your graphs look good now. You might experiment with various scaling schemes.

Instead of plotting the true magnitude $S = (S_r^2+S_\theta^2)^{1/2}$, try replacing the square root exponent of $1/2$ by other powers such as $1/4$ or $1/6$. This will keep the far fields from dying out as quickly. The contour lines will still represent lines of constant $S$, but you will get more lines at far distances.

 

[PhDeezNutz]

Made a gif

I made an MPEG4 than converted to a gif using an online movie to gif converter.

Don't know what happened to my axis though.

Maybe I shouldn't give myself a pat on the back just yet, maybe there's something wrong with it. @TSny how does it look? I kind of feel like the waves are shrinking into the origin instead of emanating from it.

 

[TSny]

Nice animation. The contour lines should propagate outwards. It could be that your time interval between images is too large. I don't know why some of your figures have only a few contour lines compared to some of the other figures.

Here are some figures at different times. I chose the unit of time to equal the period of oscillation of the dipole.

At a fixed location in the field, both E and B will reverse directions after half a period. So, $S$ will return to it's initial value after half a period. The spacing between peaks of the contour pattern (as shown by the red line segment in the t = 0 figure) is then half a wavelength of the radiation. You can see that the figure for t = 0.5 is the same as for the figure at t = 0. The pattern of contours is propagating outward at the rate of 1/2 wavelength per 1/2 period; i.e., at the speed of propagation of the waves of radiation.

 

[PhDeezNutz]

@TSny you are too helpful. I don't deserve this much help.

I'll look into these things and get back to you hopefully by tonight.

 

[PhDeezNutz]

I was able to make the waves propagate outwards by changing from $e^{i \omega t}$ to the proper $e^{-i \omega t}$

I still can’t figure out why certain frames have more contours than others. Right now I’m so desperate that I’m re-solving Jackson’s equations to confirm that they are right.

 

[TSny]

I'm fairly sure Jackson's equations are correct. I used them to get the equations for E and B in post #15 and these equations agree with what I find in a couple of other textbooks.

 

[PhDeezNutz]

I'm fairly sure Jackson's equations are correct. I used them to get the equations for E and B in post #15 and these equations agree with what I find in a couple of other textbooks.

Then I must have interpreted them wrong/ converted them wrong. I'm glad you made this post so I don't have to start from scratch.

 

[PhDeezNutz]

updated gif with waves propagating outwards as they should. Still don't know why certain frames have more contours than others.

Edit: I think it has something to do with the default way that MATLAB sets the contour levels when I specify 100 levels. It's not that the outside is truly disappearing it's that some default threshold is set that makes the outside just "blend together" and subsequently disappear.

I have to figure out how to

1) how to set custom contour levels

2) make an intelligent choice about what those contour levels would be

I could be totally off base.

Part of me thinks that setting 100 contour levels should suffice. And super weird things happen when I go to 1000 contour levels...starts to look like a quadrupole.

 

[PhDeezNutz]

Maybe there's something inherently wrong with my for loop

for i2 = 1:length(t) clf tt2 = t(i2)*ones(size(x));

Hyt2 = Hy.*exp(-1i*omega*(tt2));

Ext2 = Ex.*exp(-1i*omega*(tt2));

Ezt2 = Ez.*exp(-1i*omega*(tt2));

RealHyt2 = real(Hyt2);

RealExt2 = real(Ext2);

RealEzt2 = real(Ezt2);

Sx2 = -RealEzt2.*RealHyt2;

Sz2 = RealExt2.*RealHyt2;

Smag2 = (Sx2.^2 + Sz2.^2).^(0.5);

contour(X,Z,Smag2,100)

%Labels and such xlabel('x'); ylabel('z'); title('Poynting Vector Intensity of Oscillating Electric Dipole')

%force matlab

movieVector(i2) = getframe;end

myWriter = VideoWriter('PoyntingVectorIntensityofOSCdipole2D','MPEG-4');myWriter.FrameRate = 20;

% Open the Video Writer object write the movie and close the file

open(myWriter);

writeVideo(myWriter,movieVector);close(myWriter);

 

[TSny]

Edit: I think it has something to do with the default way that MATLAB sets the contour levels when I specify 100 levels. It's not that the outside is truly disappearing it's that some default threshold is set that makes the outside just "blend together" and subsequently disappear.

Yes, I think you'll get better plots if you specify particular values for the contour levels. I found that specifying 6 to 10 levels was sufficient.For example, the following worked pretty well:

(1) In the equations for the components of S given in post #15, I let $\frac{cp^2}{4 \pi} = 1$ and $k = \omega = 2\pi$.

(2) Instead of plotting contours of $(S_r^2 + S_\theta^2)^{1/2}$, I plotted contours of $(S_r^2 + S_\theta^2)^{1/5}$ in order to keep the far field from dying out too rapidly.

(3) I chose contour values equal to 2, 4, 6, 8, 10, 15, and 20. This seemed to work well with the choices given in (1) and (2).

(4) I plotted out to a distance of $r = 2$.

These were just arbitrary choices. You should experiment around to see what works well.

 

[PhDeezNutz]

I found out why my lines were disappearing; In each iteration of the for loop the contours are re-calibrated so to speak. To counteract that I set the scale at t = 0 and used that "set in stone scale" inside the for loop to "keep everything uniform" and make the wave look like it's traveling continuously.

Here's the result which has a few problems:

1) There's contours on the dipole axis

2) For some reason everything is real slow, I've tried changing frame rates in the range from 20 to 1000. no dice.

On the plus side

3) The radiation pattern seems to be contained within a constant "envelope" and parts of that envelope are not disappearing thankfully. Hopefully this is not a coincidence of doing something wrong.

Strangely when I use a website to convert my mp4 to a gif the gif actually turns out alright; it has a non vanishing envelope and isn't super slow. My mp4 is terrible.

edit: actually when opening my mp4 in a separate player it turns out fine. but the contours on the dipole axis are concerning.

 

[TSny]

Looks nice. The contours along the axis of the dipole are interesting. The magnitude of S is zero at all points exactly on the axis. For points near the axis, but not on the axis, S will be small but nonzero. So, if you are plotting contours with small values, then you can get some contours near the axis.

Here is a plot of contour lines near the positive z-axis over a range of about 2 to 5 wavelengths from the dipole. They seem to have some interesting strucure.

The two graphs below zoom in on this region at about 4.75 wavlengths from the dipole

 

[PhDeezNutz]

I followed your advice and filtered the smallest number from the range of S magnitudes and now the contours on the dipole axis are gone.

I have a special relativity presentation due Tuesday do you think I could incorporate this somehow? Perhaps boost it to another "nearly c" frame and see how it looks. What should I expect in such a case? (depending on which direction I boost in). I'm just thinking out loud here. I just want an excuse to continue working on this script.

(I bet that's a loaded question)

Edit: I think Jackson page 558 has the answers

 

[TSny]

Your movies are looking pretty good!

I have a special relativity presentation due Tuesday do you think I could incorporate this somehow? Perhaps boost it to another "nearly c" frame and see how it looks. What should I expect in such a case? (depending on which direction I boost in).

Yes, the radiation pattern of a relativistically moving, radiating dipole could be interesting. If the dipole moves in a direction that is perpendicular to the axis of oscillation, I think you should see some "bunching" of the contour lines out in front of the dipole corresponding to the Doppler effect. Also, it could be that the strength of the Poynting vector is increased in the forward direction. That is, maybe the radiation gets "beamed forward" at relativistic speeds.

Edit: I think Jackson page 558 has the answers

Yes, here you have the transformation equations for the fields when switching frames of reference.

 

[PhDeezNutz]

Your movies are looking pretty good!

Thank you! I couldn't have done it without your help.

Yes, the radiation pattern of a relativistically moving, radiating dipole could be interesting. If the dipole moves in a direction that is perpendicular to the axis of oscillation, I think you should see some "bunching" of the contour lines out in front of the dipole corresponding to the Doppler effect. Also, it could be that the strength of the Poynting vector is increased in the forward direction. That is, maybe the radiation gets "beamed forward" at relativistic speeds.

Yes, here you have the transformation equations for the fields when switching frames of reference.

I'll look for these patterns when making the script. I'll update this thread when I get somewhere with it.

After that my plan is to generalize my dipole script to something like the following so that I can eventually handle the quadrupole (coming up with analytical expressions for this might be hard but I hardly know anything about Finite Element Analysis so I have to come up with analytical expressions).