How do I differentiate vectors with derivatives and properties?

[KF33]

Homework Statement: The homework problem is included below, but I am looking at the derivatives of vectors.
Homework Equations: I have the properties of derivatives below, but not sure they help me here.

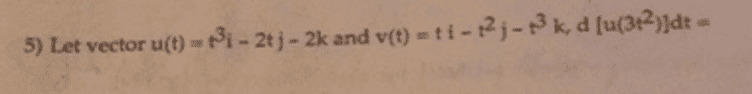https://www.physicsforums.com/attachments/249865https://www.physicsforums.com/attachments/249865

[Moderator's note: Moved from a homework forum to answer conceptional question.]

 

[fresh_42]

You have a parameterization of a vector here, i.e. a function $u\, : \,\mathbb{R}\longrightarrow \mathbb{R}^3\,.$ We want to know the differential according to the one real parameter $t$.

So first write down what $u(3t^2)$ is and simply differentiate it componentwise, since
$$
u(t)=t^3\,\mathbf{i} -2t \,\mathbf{j} -2\,\mathbf{k} = \begin{bmatrix}t^3\\-2t\\-2\end{bmatrix}
$$

 

[HallsofIvy]

One thing that complicates this is that you are using the same variable, t, in two different places. If I am reading this correctly, you have the vector function u(t)= t^3\vec{i}- 2t\vec{j}- 2\vec{k} but then you are asked to differentiate u(s^2) with respect to s (I have used "s" rather than "t" here because it is not the same variable as "t" in the definition of u).
There are two ways you can do that. One is to simply replace "t" with "s^2": u(s^2)= (s^2)^3\vec{i}- 2(s^2)\vec{j}- 2\vec{k}= s^6\vec{i}- 4s^2\vec{j}- 2\vec{k}. Differentiate that with respect to t: 6s^5\vec{i}- 8s\vec{J}. The other way is to use the chain rule: \frac{d\vec{u}}{ds}= \frac{d\vec{u}}{dt}\frac{dt}{du}= (3t^2\vec{i}- 2\vec{j})(2s), Do you see that those give the same answer?