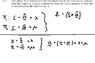Vectors: Intersection of 2 planes

[unscientific]

Homework Statement

The question is attached in the picture.

The Attempt at a Solution

I have found the direction vector of the intersection line, but I have yet to find a point that lies on both planes...

I've thought about having \hat{m} and \hat{n} as basis vectors, but i still lack 1 more vector as this question is in 3 dimensions..

OR

Since I am restricting the point to lie only on the line it can be considered as 2 dimensions?

and hence a = x\hat{m} + y\hat{n} ??

Then I can plug into the 2 plane equations and solve for x and y.

 

[Simon Bridge]

OR: work out the equations of the two planes and do it that way.

I see you tried - you end up with an equation of form \vec{u} \cdot \vec{a} = k and the problem of finding a particular \vec{a} knowing \vec{u} and k.

The difficulty is singling out just the one unique a ... you need a way to pick one out.Normally, you'd hold one coordinate constant and find the other two.
http://members.tripod.com/vector_applications/xtion_of_two_planes/index.html
... that does not help you here as you need to express your result in terms of what you are given.

But consider: you know how to find some points and lines in each plane:
p=\mu\hat{m} is the point of closest approach to the origin in plane M
q=\lambda\hat{n} is the point of closest approach to origin in plane N

What is the line through point p, in the plane M, perpendicular to the line of intersection?
What is the vector through point q, in the plane N, perpendicular to the line of intersection?

Point a will be the point of intersection between these two lines.

 

[unscientific]

OR: work out the equations of the two planes and do it that way.

I see you tried - you end up with an equation of form \vec{u} \cdot \vec{a} = k and the problem of finding a particular \vec{a} knowing \vec{u} and k.

The difficulty is singling out just the one unique a ... you need a way to pick one out.


Normally, you'd hold one coordinate constant and find the other two.
http://members.tripod.com/vector_applications/xtion_of_two_planes/index.html
... that does not help you here as you need to express your result in terms of what you are given.

But consider: you know how to find some points and lines in each plane:
p=\mu\hat{m} is the point of closest approach to the origin in plane M
q=\lambda\hat{n} is the point of closest approach to origin in plane N

What is the line through point p, in the plane M, perpendicular to the line of intersection?
What is the vector through point q, in the plane N, perpendicular to the line of intersection?

Point a will be the point of intersection between these two lines.

1)the line would be p + Ω\hat{m} (Parallel to normal of plane M)

2)The line would be q + σ\hat{n} (Parallel to normal of plane N)

The intersection of the 2 lines is at the origin. I don't see how this helps in finding point a...

 

[Simon Bridge]

What is the line through point p, in the plane M, perpendicular to the line of intersection?
What is the vector through point q, in the plane N, perpendicular to the line of intersection?

If the line is in the plane, then the line is a subset of the plane: every point on the line is also part of the plane.
If the plane in question has a normal vector n, then it must be perpendicular to n mustn't it?

[aside] I think I made a bad choice labeling one of the points "p" :(
Note: I am not going to do all your work for you. I am trying to point you in the direction of how to think about the problem that will be useful to solving it. You have to exploit the geometry of the situation in such a way to single out a single point ... the way to single out just one point in 3D is with the intersection of two lines or of three planes.

So - ferinstance - you have the direction of the line you want ... you can use that, with one of your locate-able points, to define a third plane. The intersection of the three planes will give you one point on the line.

 

[unscientific]

If the line is in the plane, then the line is a subset of the plane: every point on the line is also part of the plane.
If the plane in question has a normal vector n, then it must be perpendicular to n mustn't it?

[aside] I think I made a bad choice labeling one of the points "p" :(
Note: I am not going to do all your work for you. I am trying to point you in the direction of how to think about the problem that will be useful to solving it. You have to exploit the geometry of the situation in such a way to single out a single point ... the way to single out just one point in 3D is with the intersection of two lines or of three planes.

So - ferinstance - you have the direction of the line you want ... you can use that, with one of your locate-able points, to define a third plane. The intersection of the three planes will give you one point on the line.

1. Form a plane that contains the origin (0, 0, 0) and the 2 normal vectors \hat{m} and \hat{n}.

Thus any point on the plane would be:

r = x\hat{m} + y\hat{n}

for some x and some y.

Let r be point a where a is the intersection of this plane and the line.

Plug point a into plane M and plane N to solve for x and y.

 

[Simon Bridge]

1. Form a plane that contains the origin (0, 0, 0) and the 2 normal vectors \hat{m} and \hat{n}.

Thus any point on the plane would be:

r = x\hat{m} + y\hat{n}

for some x and some y.

Let r be point a where a is the intersection of this plane and the line.

Plug point a into plane M and plane N to solve for x and y.

... ferinstance. Yes, you can define a plane with any three points. Though you may have trouble if either λ or μ or both are zero. (Those specific cases are easy - but you want a general approach.)[edit]I thought about it - this comment is just an artifact of how you explained it. What you have there is just what I described before :)

The intersection of 3 planes is more general.

 

[ehild]

1. Form a plane that contains the origin (0, 0, 0) and the 2 normal vectors \hat{m} and \hat{n}.

Thus any point on the plane would be:

r = x\hat{m} + y\hat{n}

for some x and some y.

Let r be point a where a is the intersection of this plane and the line.

Plug point a into plane M and plane N to solve for x and y.

Yes, you can choose the vector a = xn+ym.

Keep in mind that na=λ and ma=μ,
plugging in the expression for a:
xn²+ynm=λ,
xnm+ym²=μ.
You can solve for x, y in therms of n and m.

ehild

 

[unscientific]

Yes, you can choose the vector a = xn+ym.

Keep in mind that na=λ and ma=μ,
plugging in the expression for a:
xn²+ynm=λ,
xnm+ym²=μ.
You can solve for x, y in therms of n and m.

ehild

Yup, I solved it. Thanks for the help guys!

 

[ehild]

Yup, I solved it. Thanks for the help guys!

Congrats!

ehild