- #1
MrWarlock616
- 160
- 3
Homework Statement
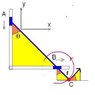
In the attached image, find angular velocity of the rod and the velocities at points B and C.
Homework Equations
vB|A=0.3ω
The Attempt at a Solution
How do I know what angle the absolute velocity makes with the other vectors when put in a triangle? How would the velocity vectors look like at point C in the attached image? It's hard for me since I only have one angle. I could calculate ω, vB, vB|A, I'm only left with vC
vB= 5.95 m/s
vB|A=7.778 m/s
Now, vC|A should be (0.3+0.15)*ω, but what do I do after that?