H Smith 94
Gold Member
- 55
- 1
Hi! I am currently trying to write a code in C to simulate the orbit of planets around the Sun in the solar system.
I am using the velocity Verlet approach and finding that my code produces no acceleration in the ##y##-direction (aside from for ##t_n = 0##,) and that the planet just flies off to infinity without finding a stable orbit.
This code produces the following output graph:
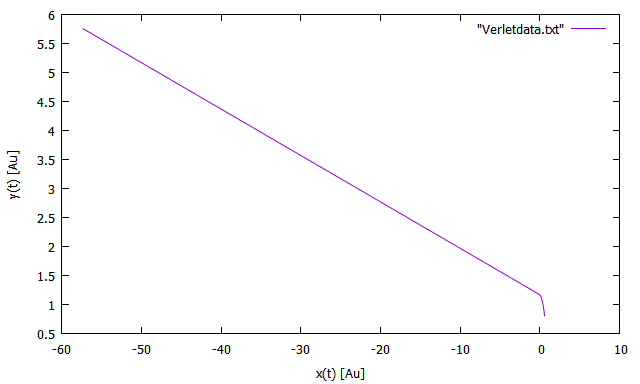
Fig. 1
Output from broken simulation showing no stable planetary orbit.
Note that the Sun is placed at (0,0) and we are examining the Earth's orbit.
I've also provided the full output file from the software as an attachment; the first few lines of diagnostics output are as follows:
Is anyone able to see where my code is going wrong? Clearly these graphs do not show a stable orbit!
I am using the MinGW GCC compiler through Eclipse Mars on Windows 8.
It's probably worth noting that this is a homework question, so I'm looking mainly for hints and advice. Thanks in advance!
I am using the velocity Verlet approach and finding that my code produces no acceleration in the ##y##-direction (aside from for ##t_n = 0##,) and that the planet just flies off to infinity without finding a stable orbit.
C:
/* INITIALIZATION */
int N = 366; // Maximum number of steps taken
if(N >= MAX_STEPS) { // Error handling
printf("N = %3i is greater than the alloted array space: %4i. \nPlease use smaller N or increase size of arrays.", N, MAX_STEPS);
exit(0);
}
double dt = 1.0 / 365.4; // Integration step
/*Initial conditions*/
t0 = 0.0;
t[0] = t0;
t[-1] = t0 - dt;
r[0] = 1.0;
th[0] = 45*deg;
x[0] = sqrt(pow(r[0],2)/(1+pow(tan(th[0]),2))); // Setting initial position of planet
y[0] = sqrt(pow(r[0],2)*pow(tan(th[0]),2)/(1+pow(tan(th[0]),2)));
double v0;
// v0 = 2.0*M_PI*Au/yr;
v0 = sqrt(G*M/r[0]);
vx0 = v0*cos(th[0]);
vy0 = v0*sin(th[0]);
// ax[0] = - (G*M/pow(r[0],2))*cos(th[0]);
// ay[0] = - (G*M/pow(r[0],2))*sin(th[0]);
x[-1] = x[0] - vx0*dt; // Defining x for pre-leap
y[-1] = y[0] - vy0*dt; // Defining y for pre-leap
printf("\tr(-1) = (%f, %f)\n",
x[-1], y[-1]);
/********************/
/* VERLET ALGORITHM */
/*__________________*/
int n; // Iteration variable
FILE *f = fopen(filename, "w"); // Opening output file in "write" mode
for(n = 0; n <= N; n++) {
r[n] = sqrt(pow(x[n],2) + pow(x[n],2));
ax[n] = - G*M*cos(th[n])/pow(r[n],2);
ay[n] = - G*M*sin(th[n])/pow(r[n],2);
x[n+1] = 2*x[n] - x[n-1] + ax[n]*pow(dt,2); // Calls function to step x from x[n] -> x[n+1]
y[n+1] = 2*y[n] - y[n-1] + ay[n]*pow(dt,2);
fprintf(f,"%3.4f\t%3.4f\t%3.4f\n",
x[n], y[n], t[n]); // Prints plot variables (x,v,t) to file
printDiagnostics(x, y, ax, ay, t, n); // Calls subroutine to print diagnostics to Console
t[n+1] = t[n] + dt; // Defines time at iteration n; discrete time Tn = n*dt
}
fclose(f); // Closing output file
return 0; // To satisfy integer requirement of function
}This code produces the following output graph:
Fig. 1
Output from broken simulation showing no stable planetary orbit.
Note that the Sun is placed at (0,0) and we are examining the Earth's orbit.
Code:
r(-1) = (0.601989, 0.792215)
n = 0 | r(0) = (0.591813, 0.806075) -> 0.836950 | a(0) = (33.353809, -45.429385) t(0) = 0.000000
n = 1 | r(1) = (0.581886, 0.819596) -> 0.822911 | a(1) = (-58.298016, -0.000000) t(1) = 0.002737
n = 2 | r(2) = (0.571523, 0.833117) -> 0.808255 | a(2) = (-60.431386, -0.000000) t(2) = 0.005473
n = 3 | r(3) = (0.560707, 0.846637) -> 0.792959 | a(3) = (-62.785279, -0.000000) t(3) = 0.008210
##\vdots## ##\vdots## ##\vdots## ##\vdots## ##\vdots## ##\vdots##Is anyone able to see where my code is going wrong? Clearly these graphs do not show a stable orbit!
I am using the MinGW GCC compiler through Eclipse Mars on Windows 8.
It's probably worth noting that this is a homework question, so I'm looking mainly for hints and advice. Thanks in advance!
Last edited:
