Visualizing the SHM of 2 blocks attached by a spring

[yucheng]

From Kleppner's Intro to Mechanics (Example 4.7, wording not exact): Two identical blocks a and b each of mass m slide without friction on a straight track. They are attached by a spring with unstretched length l and spring constant k; the mass of the spring is negligible compared to the mass of the blocks. Initially the system is at rest. At t = 0, block a is hit sharply, giving it an instantaneous velocity v 0 to the right. Find the velocity of each block at later times. (Try this yourself if there is a linear air track available—the motion is unexpected.)

After doing some Mathematics, we arrive at the formulas:

Let $\omega=\sqrt{\frac{k}{m}}$
$$v_{a}=\frac{v_{0}}{2}(1+\cos{\omega t})$$
$$v_{b}=\frac{v_{0}}{2}(1-\cos{\omega t})$$

Question 1: Does anyone have a video/animation that shows such an oscillation? I have tried searching the web but to no avail.

Question 2: Is there a general strategy to visualize such motions based on the equations? Graphs are obviously criptic: just a bunch of lines. Is there a systematic way to understand them?

I have tried using Mathematica to plot the graphs, by fixing arbitrary but still reasonable values for $v_0=6$ and $\omega=2$:

Graphs of the velocity:

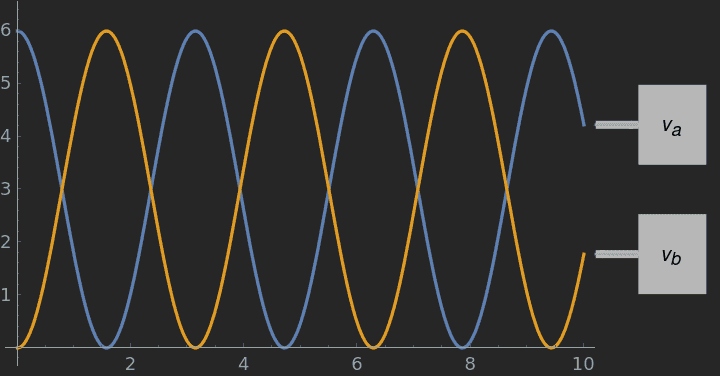
Which shows simple harmonic motion as expected.

$$x_a = \frac{6}{2} (t + 2 \sin{2 t})$$
$$x_b = \frac{6}{2} (t - 2 \sin{2 t})$$

The displacement graph? (I got it by integrating the above equations of the velocity)

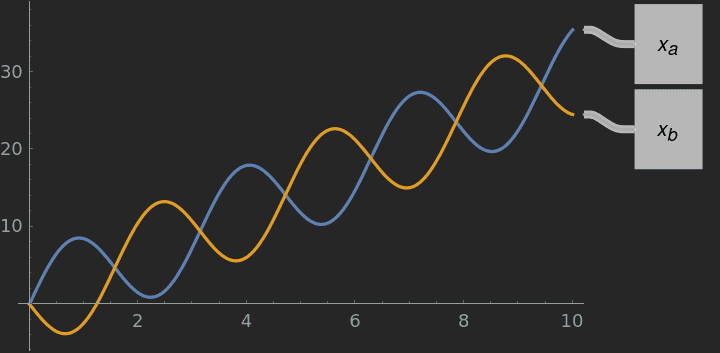
At leats it shows displacement towards the right, presumably more positive y.

Is this method correct? Obviously I am missing out on quite a few details: I am struggling to imagine the actual motion!

Thanks in advance.

 

[BvU]

Life becomes a bit more transparent in this case if you look at $v_a+v_b$ and at $v_a-v_b$ :
You 'see' motion of the center of mass and the spring oscillation

 

[yucheng]

@BvU