Wave equation, D'Alembert's Solution

[Tuneman]

I am having trouble understanding the solution to the wave equation:

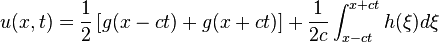
this is thought of as the final solution to the PDE:

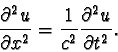
but I see that:

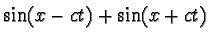
is a solution to the function. But what I don't get is why D'Alembert's Solution isn't in terms of sines and cosines like that solution right above.

Is it because D'Albemerts is a gereneral solution, and the other is a specific solution? If so, still how come the general solution to the problem isn't expressed as a wave, and instead of some arbitrary function g(x-ct)?

 

[HallsofIvy]

The general solution is a wave. But a wave is not necessarily periodic like sine or cosine. Imagine a taut rope that is distorted initially in a shape that consists of a bulge, say a triangle between x= -1 and x= 1, given by y= x+1 for x<0, y= 1-x for x>=0 and then released from rest at t=0. "g" splits into two parts which move right and left: that's what (1/2)g(x-ct) and (1/2)g(x+ct) are. The h integral allows non-zero speed at t= 0 also.