Webpage title: How to Find the Area Bounded by Curves on a Given Interval

[noboost4you]

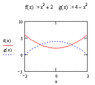
This is the problem: find the area of the region bounded by the curves f(x) = x^2 + 2 and g(x) = 4 - x^2 on the interval [-2,2]

I did the whole integral from -2 to 2 with (4-x^2) - (x^2 + 2) dx because the graph of g(x) is on top between the region bounded. But from my drawing, the points where the curves meet and shaded in the area is between -1 and 1. What am I doing wrong?

My answer came to be -8/3 and area can't be negative. Any suggestions?

Thanks

 

[pnaj]

It's a of an ambiguous question ... see my attached image. Check that question for typo's, just in case.

 

[noboost4you]

no typos here. he wrote this problem on the board today, maybe he has it wrong?? the question never says anything about the area under the curves, just the region bounded by the curves on the interval [-2,2]. maybe i need to draw imaginary vertical lines at -2 and 2 and include that area as well as under the curves?

i'm lost and it's only the 2nd day of class...oohh, i can't wait until the 3rd day

 

[pnaj]

Don't worry. I'm sure if you pointed out the confusion, he'll tell what he meant.

 

[noboost4you]

So as it stands right now, that equation is impossible to answer? Correct?

 

[HallsofIvy]

I wouldn't say it was impossible, just ambiguous as to exactly what was being asked. Since the problem asks for "area bounded by the curves between -2 and 2, I would say it must be:

∫_-2^-1((x²+2)-(4-x²)dx+ ∫_-1¹((4-x²)-(x²+2))dx+ ∫₁²((x²+2)-(4-x²))dx.

That is, reverse the subtraction on the two ends where the curves are reversed.

 

[nille40]

The area bounded by f(x) and g(x) where a \le x \le b is given by

<br /> \int_a^b \left|f(x)-g(x)\right|\mathrm{d}x<br />

Consider the integral
<br /> \int_{\pi}^{2\pi} \sin x \mathrm{d}x<br />

The graph is below the x-axis, so the value will be negative. An area can't be negative, so you just take the absolute value of it.

Regards,
Nille

 

[IceZero]

What I am guessing he wanted you to do is to include the two areas on each side of the curves...So include the area from -2 to -1 from -1 to 1 and from 1 to 2... Thats what I prob would do...So then you would have three separate integrals 2 of which should be the same area...and one different one in the middle..

Just my 2 cents...

 

[noboost4you]

Yes, the answer included 3 separate integrals. The final solution came to 8. Thanks to all who helped out. I really appreciate it.

 

[IceZero]

No problemo my friend...I though it would include 3 separate integrals otherwise he wouldn't have given you intervals...If he didn't give u intervals then you would only have one integral from -1 to 1...But since he told you that you have interval from -2 to 2,then you would have to sketch the graph, see how it looks, and then come up with the fact that there is actually 3 separate areas which need to be added...

I am glad you solved your problem. :)