tizzful
- 14
- 0
Weight and Wheel ! (Linear and Angular Acceleration)
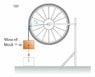
Consider a bicycle wheel that initially is not rotating. A block of mass is attached to the wheel and is allowed to fall a distance . Assume that the wheel has a moment of inertia, I, about its rotation axis.
A)Consider the case that the string tied to the block is attached to the outside of the wheel, at a radius ,ra. Find the angular speed of the wheel after the block has fallen a distance h, for this case.
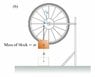
b)Consider the case that the string tied to the block is attached to the outside of the wheel, at a radius ,rb. Find the angular speed of the wheel after the block has fallen a distance h, for this case.
K=1/2mv^2 U=mgh Mechanical energy conserved therefore E=K+U
V=rw
Images attached
(a)U1+K1=U2+K2
mgh+0=0+1/2mv^2+1/2Iw^2
2mgh=mv^2+Iw^2
2mgh=mv^2+I(V/r)^2
(2mghr^2)/(mr^2+I)=v^2
V=SQRT((2mghr^2)/(mr^2+I))
w=v/r
w=SQRT((2mghr^2)/(mr^2+I))/r
(b) the same? just changing the r values?
I entered that as my answer but it says that it does not depend on the variable m and r but the only way to get rid of them is if the moment of intertia wasn't I.. So now I'm very confused and have no way of figuring out how to cancel them...
Help?
Thank you!
Homework Statement
Consider a bicycle wheel that initially is not rotating. A block of mass is attached to the wheel and is allowed to fall a distance . Assume that the wheel has a moment of inertia, I, about its rotation axis.
A)Consider the case that the string tied to the block is attached to the outside of the wheel, at a radius ,ra. Find the angular speed of the wheel after the block has fallen a distance h, for this case.
b)Consider the case that the string tied to the block is attached to the outside of the wheel, at a radius ,rb. Find the angular speed of the wheel after the block has fallen a distance h, for this case.
Homework Equations
K=1/2mv^2 U=mgh Mechanical energy conserved therefore E=K+U
V=rw
Images attached
The Attempt at a Solution
(a)U1+K1=U2+K2
mgh+0=0+1/2mv^2+1/2Iw^2
2mgh=mv^2+Iw^2
2mgh=mv^2+I(V/r)^2
(2mghr^2)/(mr^2+I)=v^2
V=SQRT((2mghr^2)/(mr^2+I))
w=v/r
w=SQRT((2mghr^2)/(mr^2+I))/r
(b) the same? just changing the r values?
I entered that as my answer but it says that it does not depend on the variable m and r but the only way to get rid of them is if the moment of intertia wasn't I.. So now I'm very confused and have no way of figuring out how to cancel them...
Help?
Thank you!