Weird idea (gradients and potentials)

[DivergentSpectrum]

So, a while back i read about this idea, but i can't find it anymore, so i was wondering if anybody else knows about it. here it is:

We know that if a vector field is conservative, then there exists some surface whos level curves are perpendicular to the vector field. or inversely, that the vector field grad(f) is pointing in the direction of highest increase of f.

Heres the shocker: unlike what you were told, even if a vector field is non conservative there still is some surface that cooresponds to it.

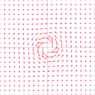
I attached some pictures, one of an obviously non-conservative vector field (see the rotation?)
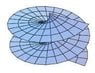
and one of a surface.

It seems to me, that the vector field shown is pointing in the direction of the highest increase of the surface given by the function z(x,y) . (note that these arent exact representations, they are just some pics i pulled off of google image search.)

I also realize, that the potential "function" shown isn't actually a function at all, according to my high school algebra teacher. The surface keeps spiraling around the z axis so there are multiple values for z at each point x and y. This isn't unheard of, for example sqrt(1)=1 and -1, so there should be some way to work around it.

I know all i really have here is a visual/intuitive argument, and maybe it is just an optical illusion, but I am really starting to think that a non conservative vector field may be the gradient of a multi-valued function. Who else knows about this? what does it mean? Does it have any applications(ie maxwells laws for magnetism)?

 

[Simon Bridge]

If the vector field is non-conservative, you can still have scalar potentials for them, it's just harder.
I found a lecture - just slides though.
http://www-astro.physics.ox.ac.uk/~sr/lectures/multiples/Lecture7reallynew.pdf
... usually you end up with a "vector potential" rather than a scalar potential.

 

[Incnis Mrsi]

bluntwcrackrap: you probably going to rediscover contact geometry, but Euclidean-specific identification of vector fields with 1-forms makes me unable to get into your reasoning.

 

[DivergentSpectrum]

i looked it up, and found that the surface is called a helicoid, and its equation is given by
z(x,y)=c*atan(y/x)

then ∂z/∂x=-cy/(x²+y²)
and ∂z/∂y=cx/(x²+y²)
this gradient is obviously a rotational vector field, as you can see in the pic

so i did ∇χ∇z(curl of gradient)=

d(-cy/(x²+y²))/dy-d(cx/(x²+y²)/dx=0

so, i guess i was wrongly associating rotational with nonconservative... i graphed it and its obviously a rotational vector field, but supposedly its also conservative? this makes no sense! if i calculated the line integral of this field it would clearly be different if i did it clockwise instead of counterclockwise...
man, right when i thought i understood multivariable calculus...

i also tried doing the line integral, and i am convinced i broke math, because any attempt to do a line integral of the field over a portion of a circular arc equals zero (which makes no since because my eyes tell me a circular path would be parallel to the vector field everywhere) and now i have to figure out some other curve to integrate over

 

[DivergentSpectrum]

whoops, i did the integral wrong.

[-csint/(cost²+sint²),ccost/(cost²+sint²)]*[-sint,cost]=c
∫c dt=c(t1-t0).
if i took the integral from 0 to 2*pi, i get c*2pi, the opposite if i had gone the other way.
i decided the find the div of this field, and incidently it equals 0.

well, i did what i set out to do, but I am kinda left with this unfulfilled feeling. what kind of weird things are going on here?

 

[DivergentSpectrum]

The contact geometry thing kinda went over my head, lol
The pdf didnt seem to really discuss this.

It appears i made some mistakes (figures lol) in the calculations.
the vector field
[-cy/(x2+y2),cx/(x2+y2)] is NONCONSERVATIVE
curl=-c*ln(x^2+y^2)
it is also the gradient of the surface z(x,y)=c*atan(y/x)

I really think this is a deep result. i know it may seem like I am trying to break math, but I am interested in "how" it breaks. obviously we have asymptotes where x=0. (z will jump from -pi/2 to pi/2)
still its really fascinating.
i was wondering maybe i could generalize this to any vector field? if this is the case with the helicoid, maybe all nonconservative vector fields are gradients of different types of asymptotic/multivalued surfaces?

what if there was a function f(x,y,z) that had a nonconservative gradient?

so anyway, lots of questions here
thanks

 

[DivergentSpectrum]

could a mod please delete my last post (i second guessed myself and was wrong)
the curl of the vector field [-c*y/(x²+y²),c*x/(x²+y²)] does equal 0
but its non-conservative! its actually rotational. if i do a line integral on a circle clockwise centered at the origin i will get the opposite of if i did it counterclockwise

so what does 0 curl mean exactly?
we have to amend the definition that 0 curl means conservative.

i know it seems like I am trying to break math, but i want to know "how" it breaks.
i think its amazing how the asymptotes of the helicoid are "mapped" to its gradient to create paradoxes.
(with the helicoid z(x,y)=c*atan(y/x) we obviously have an asymptote at x=0 where z will jump between -pi/2 and pi/2)
if i just looked at this vector field with no knowledge that it is the gradient of a helicoid, it would be very perplexing!

 

[AZW]

I believe 0 curl implies conservative if and only if your domain is simply connected. In your case the field has a singularity at 0.
http://en.wikipedia.org/wiki/Conservative_vector_field

 

[DivergentSpectrum]

hmm, so basically what youre saying is that even though there are no asymptotes in the vector field itself (besides at x=0,y=0,which is trivial), the fact that the vector field is the gradient of an asymptotic surface is enough to make the vector field nonconservative but with 0 curl.

fascinating

 

[Dlop]

Check this paper: (Page 603); "Thus, any vector field may be represented as the gradient of a scalar function, the function being multivalued if the vector field is non-conservative."
Dave Pandres, JR., Journal of Mathematical Physics, Vol. 3, page 602 (1961)

http://dx.doi.org/10.1063/1.1724263