JungleJesus
- 36
- 0
I am reading Visual Complex Analysis by Dr. Tristan Needham and am hung up on some of the geometrical concepts. In particular, I am having trouble with ideas involving the geometric properties of numbers like:
\frac{z-a}{z-b}
Note: I am still in the first and second chapters, which deal with the basic geometry of complex numbers and functions.
As an example problem, here is one I've been trying to figure out for a few days:
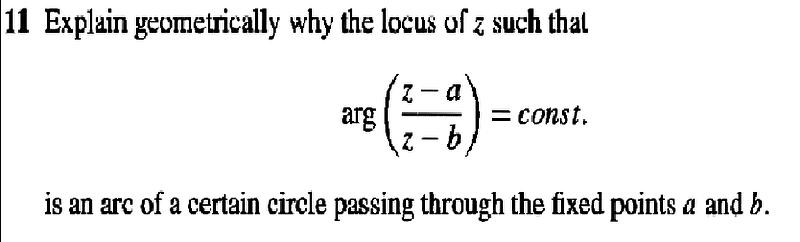
As an attempted solution, I chose three arbitrary points a, b, z and constructed the perpendicular bisector of a and b and a three point circle through a, b and z. The chord through a and b divides the circle into two regions.
Since z is a variable under a constraint, it may move freely about this circle. As long as z stays on the same side of chord \stackrel{\rightarrow}{ab}, the angle between the chords \stackrel{\rightarrow}{az} and \stackrel{\rightarrow}{bz} will be a constant. I interpreted (but have found no way to prove) the constant angle as the constant referred to in the problem.
That being said, it looked to me like the tangent of this angle was equal to Im((z-a)/(z-b))/Re((z-a)/(z-b)),
where Im(z) and Re(z) are the imaginary and real parts of the complex number z.
This is as far as I got. I showed that the angle between chords was constant along the three point circular arc of a, b and z. I have no idea if this is even the right place to look, and this problem is only one of many dealing with complex ratios that I simply don't understand.
Any help?
\frac{z-a}{z-b}
Note: I am still in the first and second chapters, which deal with the basic geometry of complex numbers and functions.
As an example problem, here is one I've been trying to figure out for a few days:
As an attempted solution, I chose three arbitrary points a, b, z and constructed the perpendicular bisector of a and b and a three point circle through a, b and z. The chord through a and b divides the circle into two regions.
Since z is a variable under a constraint, it may move freely about this circle. As long as z stays on the same side of chord \stackrel{\rightarrow}{ab}, the angle between the chords \stackrel{\rightarrow}{az} and \stackrel{\rightarrow}{bz} will be a constant. I interpreted (but have found no way to prove) the constant angle as the constant referred to in the problem.
That being said, it looked to me like the tangent of this angle was equal to Im((z-a)/(z-b))/Re((z-a)/(z-b)),
where Im(z) and Re(z) are the imaginary and real parts of the complex number z.
This is as far as I got. I showed that the angle between chords was constant along the three point circular arc of a, b and z. I have no idea if this is even the right place to look, and this problem is only one of many dealing with complex ratios that I simply don't understand.
Any help?