StevieTNZ
- 1,934
- 873
From a previous post, I now know that the 'qualities' of QM such as entanglement, superposition of states, decoherence, measurement problem, are still with us in QFT.
1. Is the Dirac equation the primary equation in QFT?
2. What equation governs the evolution of a macroscopic object in QFT?
3.
I found this http://en.wikipedia.org/wiki/Newton–Wigner_localization, but doesn't that only apply to single particle? Is it even an equation?
and one final question:
How do you write all the possible states of a quantum system in QFT?
e.g.
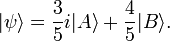
1. Is the Dirac equation the primary equation in QFT?
2. What equation governs the evolution of a macroscopic object in QFT?
3.
How does one calculate the superposition of positions for a microscopic or macroscopic object in QFT? Does that equation evolve in the same way as the Schrodinger Equation?In quantum field theory, unlike in quantum mechanics, position is not an observable, and thus, one does not need the concept of a position-space probability density.
I found this http://en.wikipedia.org/wiki/Newton–Wigner_localization, but doesn't that only apply to single particle? Is it even an equation?
and one final question:
How do you write all the possible states of a quantum system in QFT?
e.g.