What Are the Normal and Shear Stresses on the Inclined Butt Weld?

[Zouatine]

Homework Statement

Calcul of stresses

Relevant Equations

1- σ'x=σx*cos(β)^2+σy*sin(β)^2+2*τxy*cos(β)*sin(β)

2- σ'y=σx*sin(β)^2+σy*cos(β)^2-2*τxy*cos(β)*sin(β)

3- τxy'=-σx*sin(β)*cos(β)+σy*sin(β)*cos(β)+τxy*(cos(β)^2-sin(β)^2)

Hi! i have this exercise and solution :

Exercise:
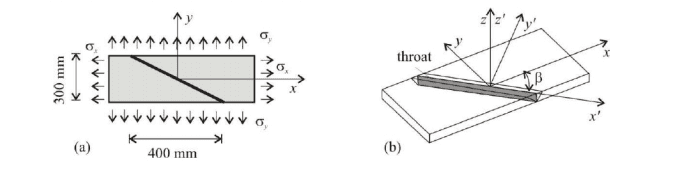
steel plate given in figure (a) is joined by an inclined butt weld ,the plate is subjected to tensile stresses in both x and y directions, σ(x)=54 N/mm^2 and σ(y)=38 N/mm^2 ,
1) Determine the normal and shear stresses of the butt weld.

this is transformation matrices :

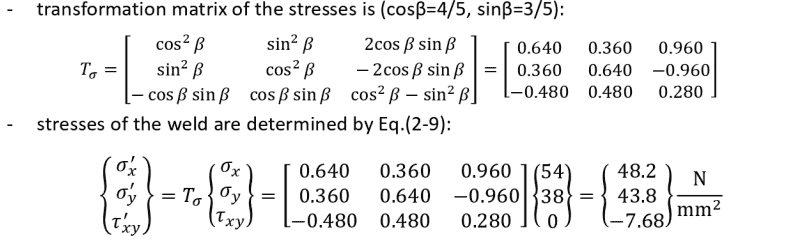
2)second question :
in which direction the stress normal will be maximum ?

My problem: is τxy ( why in first we made it 0 in transformation matrice (and why it's 0) and in second question it's calculed .

 

[haruspex]

As far as I can make out, the first part is a calculation for a special case where there is no applied torque, whereas the second finds the weld direction that maximises stress in the more general case.

 

[Chestermiller]

In this system, the stress tensor is given by$$\boldsymbol{\sigma}=\sigma_x\mathbf{i_x}\mathbf{i_x}+\sigma_y\mathbf{i_y}\mathbf{i_y}$$and the unit normal to the weld is given by: $$\mathbf{n}=\sin{\beta}\mathbf{i_x}+\cos{\beta}\mathbf{i_x}$$So the traction vector on the weld is given by: $$\boldsymbol{T}=\boldsymbol{\sigma}\centerdot \mathbf{n}=\sigma_x \sin{\beta}\mathbf{i_x}+\sigma_y \cos{\beta}\mathbf{i_y}$$The normal component of the traction vector on the weld is equal to the traction vector dotted with the unit normal: $$\sigma_n=\boldsymbol{T}\centerdot \mathbf{n}=\sigma_x \sin^2{\beta}+\sigma_y\cos^2{\beta}=\frac{(\sigma_x+\sigma_y)}{2}-\frac{(\sigma_x-\sigma_y)}{2}\cos{2\beta}$$The unit tangent vector to the weld is given by $$\mathbf{t}=\cos{\beta}\mathbf{i_x}-\sin{\beta}\mathbf{i_y}$$The shear component of the traction is obtained by dotting the traction vector with the unit tangent:$$\tau=(\sigma_x-\sigma_y)\sin{\beta}\cos{\beta}=\frac{(\sigma_x-\sigma_y)}{2}\sin{2\beta}$$