Minusu
- 8
- 0
I've tried these problems but I just can't wrap my head around them. Thanks to anyone that can help me out here. I have a couple more problems similar to these to solve, but if I can get to understand these then I'll have no problem with the others.
Here are some diagrams I drew: http://gyazo.com/bf78da97179aa8d62d5e44b484ffcdc3 and http://gyazo.com/65689d4a0de1f23ceeae3c236c1c891e
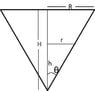
1. Homework Statement :
A conical paper cup is 30cm tall with a radius of 10cm. The cup is being filled with water a rate of 16*pi/3 cm^3/sec. How fast is the water level rising when the water level is 6cm?
dV/dt = 16*pi/3
r=10
h=30
hw(height of water)=6
dh/dt=?
2. Homework Equations :
V=1/3*pi*r^2*h
3. The Attempt at a Solution :
V=1/3*pi*r^2h
dV/dt=1/3*pi*r^2*dh/dt
16*pi/3=1/3*pi*10^2*dh/dt
3/100*pi *16*pi/3=100*pi/3dh/dt *3/100*pi
16*pi/100*pi=dh/dt
16/100=dh/dt
1. Homework Statement :
A 7 ft tall person is walking away from a 20 ft tall lamppost at a rate of 6/x ft/sec, where x is the distance from the person to the lamppost. Assume the scenario can be modeled with right triangles. At what rate is he length of the person's shadow changing when the person is 15 ft from the lamppost?
y= height of lamppost, 20ft
x= distance from lamppost to person, 15 ft
dx/dt= 6/15
2. Homework Equations :
a^2 + b^2 = c^2
3. The Attempt at a Solution :
x^2 + y^2 = c^2
2x*dx/dt + 2y*dy/dt = 0
2*15*(6/15) + 2*20*dy/dt = 0
12+40dy/dt=0
dy/dt = -12/40
Here are some diagrams I drew: http://gyazo.com/bf78da97179aa8d62d5e44b484ffcdc3 and http://gyazo.com/65689d4a0de1f23ceeae3c236c1c891e
1. Homework Statement :
A conical paper cup is 30cm tall with a radius of 10cm. The cup is being filled with water a rate of 16*pi/3 cm^3/sec. How fast is the water level rising when the water level is 6cm?
dV/dt = 16*pi/3
r=10
h=30
hw(height of water)=6
dh/dt=?
2. Homework Equations :
V=1/3*pi*r^2*h
3. The Attempt at a Solution :
V=1/3*pi*r^2h
dV/dt=1/3*pi*r^2*dh/dt
16*pi/3=1/3*pi*10^2*dh/dt
3/100*pi *16*pi/3=100*pi/3dh/dt *3/100*pi
16*pi/100*pi=dh/dt
16/100=dh/dt
1. Homework Statement :
A 7 ft tall person is walking away from a 20 ft tall lamppost at a rate of 6/x ft/sec, where x is the distance from the person to the lamppost. Assume the scenario can be modeled with right triangles. At what rate is he length of the person's shadow changing when the person is 15 ft from the lamppost?
y= height of lamppost, 20ft
x= distance from lamppost to person, 15 ft
dx/dt= 6/15
2. Homework Equations :
a^2 + b^2 = c^2
3. The Attempt at a Solution :
x^2 + y^2 = c^2
2x*dx/dt + 2y*dy/dt = 0
2*15*(6/15) + 2*20*dy/dt = 0
12+40dy/dt=0
dy/dt = -12/40