What Are the Spring and Friction Constants for a Small Truck's Shock Absorbers?

[JulienB]

Homework Statement

Hi everyone! I'm still trying to make my way through the wonderful land of oscillations. That's going to take a while.

The springs and shock absorbers of a small truck have been conceived, so that the truck body sinks of a distance s = 100mm by full load (total mass m = 1.8 t) and that the wheels (mass m_R = 40 kg) oscillate in aperiodic damping. The four wheels carry the same amount of weight and each wheel has its own spring and shock absorber. Consider a general damping force F_R = -b⋅v.
How big must the spring constant k and the friction constant b of a shock absorber be?

Homework Equations

Newton, oscillations

The Attempt at a Solution

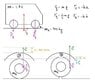
I attempted to solve this old homework using what another student did. There are a few obscure points I'd like to ask your opinion about, so that I can better understand them. Please check the attached photo to have a visualisation of how I conceive the situation in my head.

I would like to start with a question: does "aperiodic damping" refer to "critically damped"? I translated the problem from German, so I'm not sure but that's what I assumed when solving the problem.

So first I think that by full load and no oscillation, the forces of gravity (I named F'_g the force of gravity acting on one wheel) and spring are balanced and there is no damping force:

ΣF = 0 ⇔ F'_g = F_F
⇔ ¼⋅m⋅g = -k⋅s
I solve for k:
k = m⋅g/4⋅s = 44100 N⋅m^-1

To get b, I thought the first thing to do was to set up an equation of motion for one wheel:

m_R⋅a = ¼⋅m⋅g + k⋅x - b⋅dx/dt
⇔ m_R⋅d²x/dt² + k⋅s - k⋅(x + s) + b⋅dx/dt = 0
⇔ m_R⋅d²x/dt² + k⋅x + b⋅dx/dt = 0
⇔ d²x/dt² + (k/m_R)⋅x + (b/m_R)⋅dx/dt = 0

Hopefully this is correct. Now I saw on wikipedia that the next step is to define the natural frequency ω₀ = √(k/m_R). Why do we do so? Do we really define it? Anyway I can then write the equation of motion as:

d²x/dt² + ω₀²⋅x + (b⋅ω₀/k)⋅dx/dt = 0

And now comes a step I don't really understand. Apparently from the equation of motion (but maybe not) follows:

b/m_R = 2⋅ω₀

What? Where does that come from? Is it because the oscillation is critically damped? I saw (on wiki, again) that for the case of a critically damped system, b/(2√(mk)) = 1 which basically leads to the same result but without having to define ω₀.

Hopefully someone can help me understand that step, while I hope the previous calculations are correct.

Thank you very much in advance.Julien.

 

[drvrm]

Now I saw on wikipedia that the next step is to define the natural frequency ω0 = √(k/mR). Why do we do so? Do we really define it? Anyway I can then write the equation of motion as:

from wiki
ω0 is the undamped angular frequency of the oscillator and ζ is a constant called the damping ratio. This equation is valid for many different oscillating systems, but with different formulas for the damping ratio and the undamped angular frequency.


The value of the damping ratio ζ determines the behavior of the system such that ζ = 1 corresponds to being critically damped with larger values being overdamped and smaller values being underdamped. If ζ = 0, the system is undamped.

actually one has a differential equation with a term proportional to velocity and the easier way to analyse it is -in terms of undamped frequency which has a well known nature and if one superimposes a solution on it taking the damping coefficient
the actual /real solution comes out as a function of the undamped frequency- that is the advantage. one does the same exercise for forced oscillations.

 

[JulienB]

@drvrm Thank you very much for your answer. Does that mean that anytime I have to deal with a simple harmonic motion, the undamped frequency ω₀ is going to be √(k/m)? Maybe that is even the "definition" of SHM so to say?Julien.

 

[drvrm]

Does that mean that anytime I have to deal with a simple harmonic motion, the undamped frequency ω0 is going to be √(k/m)? Maybe that is even the "definition" of SHM so to say?

As i understand the SHM's its representative equation is Force= - k . displacement ;
therefore the 2nd order differential equation is regular with no in homogeneous terms.
k may differ from system to system but all further involvement of terms in the differential equation- will lead to superposition of particular solutions on the base of pure SHM's- the frequency w0is a good characteristic of the nature of oscillatory systems.

 

[JulienB]

@drvrm thank you that was a very good explanation.