SUMMARY
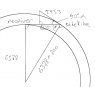
The discussion centers on the discrepancies in Doppler shift calculations for satellites in orbit, specifically addressing a satellite at 800 km altitude. Participants calculated the satellite's relative velocity as 6720 m/s, while the expected orbital speed is 7453 m/s. The difference in values, which participants initially thought should be around 465 m/s due to Earth's rotation, turned out to be nearly double. Key calculations involved using the formula for relative velocity and considering the angle between the satellite and the receiver on the ground.
PREREQUISITES
- Understanding of Doppler shift principles in satellite communications
- Familiarity with orbital mechanics and satellite velocity calculations
- Knowledge of trigonometric functions and their application in relative motion
- Proficiency in using formulas for relative velocity and orbital speed
NEXT STEPS
- Study the derivation of the Doppler shift formula: v = -Δf c / f0
- Explore orbital mechanics, focusing on the calculation of orbital speed using v = √(GM / (R + h))
- Investigate the effects of receiver position on Doppler shift measurements
- Learn about the impact of Earth's rotation on satellite communication frequencies
USEFUL FOR
Amateur radio operators, satellite communication engineers, and students of physics interested in understanding Doppler effects in satellite transmissions.