What Determines the Resolution Limit of a Microscope?

[eoghan]

Hi there!
I wonder where the resolution limit for a microscope comes out. I know that the lens can act as a circular aperture of diameter D and so a point source is diffracted in a disk of angular aperture 1.22\lambda/D
Two sources are resolved if their distance is greater than (without Abbe correction) 1.22\lambda/NA
How can I obtain this result?
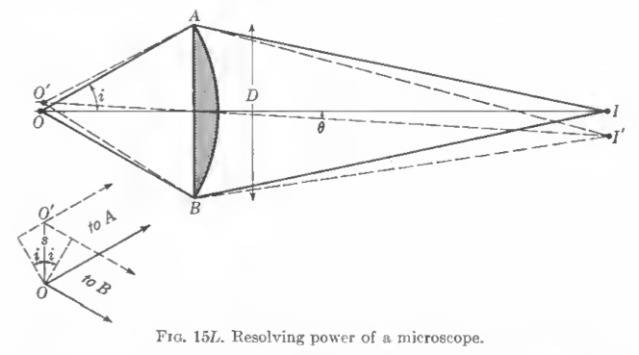
I'm reading Jenkins and White and they start supposing two point sources, O on the axis of the lens and O' slightly above which form images I and I'. Each image consists of a disk and the angular separation of the disks when they are on the limit of resolution is 1.22\lambda/D
When this condition holds, the wave from O' diffracted to I has zero intensity and the extreme rays O'BI and O'AI differ in path by 1.22lambda. (B is the top point of the lens, and A is the lower point; I is the position of the image of O and lies on the lens axis) Why do they differ in path by 1.22lambda?

I also attach the image, taken from the book, of the geometry

 

[DrDu]

I suppose you have to derive first the size of the Airy disk in the focal plane. The rest is geometry.

 

[eoghan]

I tried, but I'm not sure. The distance II' is
II'=f\sin(\theta)
where f is the distance of I from the center of the lens.
The images are resolved if
II'\geq f\frac{1.22\lambda}{D}
If we call f' the distance between O and the center of the lens, we have
\frac{OO'}{f'}=\frac{II'}{f}
therefore at the limit of the resolution
\frac{OO'}{f'}=\frac{f\frac{1.22\lambda}{D}}{f}
But from the geometry we know that
f'=\frac{\frac{D}{2}}{\tan(i)}\simeq\frac{D}{2sin(i)}
Thus, in the end
OO'=\frac{1.22\lambda}{2\sin(i)}

Is this all right? My doubt is that this derivation is much simpler than that given in textbook...

 

[Andy Resnick]

It may help to realize that angular resolution and linear resolution are related through the focal length of the lens 'f' and NA = D/2f (approximately).