What Equation Should I Use for Calculating Total Impedance in RLC Circuits?

[Mrhu]

Homework Statement

Hello again!

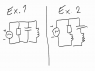
We have been given a couple of more advanced problems where the components are placed in series parallely.

Check the image, the question is regarding what equation to use, in order to calculate the total impedance of the circuit.

Homework Equations

I have stumbled upon the following equations...
$Z_{tot}$=$\frac{1}{\frac{1}{Z_{1}}+\frac{1}{Z_{2}}}$

And the same equation, only squared and partly modified

$Z_{tot}$=$\frac{1}{\sqrt{(\frac{1}{R})^{2}+(\frac{1}{X_{L}}-\frac{1}{X_{C}})^{2}}}$

The Attempt at a Solution

If you take a look at the image you will see two examples, my theory is that the second equation is valid for the first example.

But when does one use the first equation? And can the second equation be used on the second example, and vice versa?

Many thanks in advance, please do use real numbers when explaining. I am aware of the importance of complex numbers in RLC circuits we have not applied them in Physics yet.

 

[ehild]

The first equation refers to the complex resultant impedance Z if two complex impedances, Z1 and Z2 are connected in parallel. The second one shows the magnitude Z of the resultant impedance of parallel connected resistor, capacitor and inductor. The identical notation is confusing.



ehild

 

[Mrhu]

The first equation refers to the complex resultant impedance Z if two complex impedances, Z1 and Z2 are connected in parallel. The second one shows the magnitude Z of the resultant impedance of parallel connected resistor, capacitor and inductor. The identical notation is confusing.



ehild

Thank you for the quick reply.

Yes, it is a bit confusing.

If you look at the picture (example 2), should I first calculate the part-impedances, then add them using the first equation in order to achieve the total impedance?

Thanks ehild

 

[ehild]

You can not solve example 2 without using complex impedances. Yes, you need to calculate the complex Z1 and Z2 separately, then add them as complex numbers, according to the first equation.

$$\hat Z_1=R+iX_L$$

$$\hat Z_2=i(X_L-X_C)$$

The reciprocal impedances add up:

$$\frac{1}{\hat Z}=\frac{1}{\hat Z_1}+\frac{1}{\hat Z_2}$$

You get the magnitude by multiplying by the complex conjugate and then take the square root.

ehild