What force is needed to push out this slab on the bottom of the stack?

[Lotto]

Homework Statement

I have three slabs put on themselves. Coeficient of friction among them is $\mu$ and between the slab touching the ground and the ground also $\mu$. What minimal force do I need to push the last slab out of the two ones?

Relevant Equations

The correct equation is according to the solution $mg\mu=F-5mg\mu$.

The picture is here:

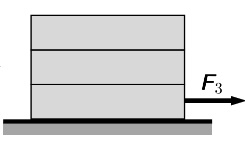
I understand that friction I need to overcome is $5mg\mu$, but why do I need to accelerate the slab on acceleration $g\mu$?

 

[erobz]

I understand that friction I need to overcome is $5mg\mu$, but why do I need to accelerate the slab on acceleration $g\mu$?

Have you examined whether or not if you simply let $F - 3 \mu M g > 0$ whether or not either/both of the other blocks would accelerate with the lower block when $F$ was applied?

Spoiler: Hint:

Think about the maximal acceleration the static friction forces could supply to each of the upper blocks before slipping (between blocks) is initiated.

 

[Lotto]

Have you examined whether or not if you simply let $F - 5 \mu M g > 0$ whether or not either/both of the other blocks would accelerate with the lower block when $F$ was applied?

Spoiler: Hint:

Think about the maximal acceleration the static friction forces could supply to each of the upper blocks before slipping (between blocks) is initiated.

It's clear to me that the maximal acceleration is $\mu g$, but how is it related to the problem? When I calmly apply force $6mg\mu$, the system has that acceleration and is moving. When I apply the force in a very short time, then I pust the block out. But why do I need to apply that force?

If I apply force $5mg\mu$ in a very short time, what will happen? Nothing I guess? And when I apply force a little bigger than $5mg\mu$, shouldn't I push the block out?

 

[erobz]

If I apply force $5mg\mu$ in a very short time, what will happen? Nothing I guess? And when I apply force a little bigger than $5mg\mu$, shouldn't I push the block out?

If you apply up to $3 \mu M g$ nothing will happen ( do you see its not $5 \mu M g$? - I got that wrong not thinking critically in my first reply so I've edited it ) . If $3 \mu M g < F \leq 6 \mu Mg$ what happens? Ask yourself if the static friction forces acting in between the blocks can carry the upper blocks along with the lower block at $0< a \leq a_{max}$? If you find out they can be carried along without slipping relative to each other, then the bottom block is not being pulled out from under the other two, its simply carrying them along for the ride.

Remember $a_{max}$ is a constraint not on the bottom block, but on the upper blocks, because of frictional limitations between them. In effect, they are "glued" to each other and the lower block until the "glue breaks". The "glue" breaks when the static friction forces between them are maximal, at which point they slip relative to each other.

$$ 0 \leq f_s \leq \mu_s N $$

 

[erobz]

For example, solve for the acceleration $a$ of the entire system if $F= 4 \mu M g$. What is $a$, compared to $a_{max}$ ( the acceleration that would - if exceeded - "break the glue" between the top block and the one directly beneath it for instance)?

 

[Lotto]

If you apply up to $3 \mu M g$ nothing will happen ( do you see its not $5 \mu M g$? - I got that wrong not thinking critically in my first reply so I've edited it ) . If $3 \mu M g < F \leq 6 \mu Mg$ what happens? Ask yourself if the static friction forces acting in between the blocks can carry the upper blocks along with the lower block at $0< a \leq a_{max}$? If you find out they can be carried along without slipping relative to each other, then the bottom block is not being pulled out from under the other two, its simply carrying them along for the ride.

Remember $a_{max}$ is a constraint not on the bottom block, but on the upper blocks, because of frictional limitations between them. In effect, they are "glued" to each other and the lower block until the "glue breaks". The "glue" breaks when the static friction forces between them are maximal, at which point they slip relative to each other.

$$ 0 \leq f_s \leq \mu_s N $$

Can I imagen it using an non-inertial frame of reference? If I am connected with the bottom block and want to see the two blocks start to move, then they has to gain an inertial acceleration of $\mu g$, so I has to accelerate with the block relative to earth with the same magnitude, thus $F-5mg\mu=mg\mu$.

Is this idea correct?

 

[erobz]

Can I imagen it using an non-inertial frame of reference? If I am connected with the bottom block and want to see the two blocks start to move, then they has to gain an inertial acceleration of $\mu g$, so I has to accelerate with the block relative to earth with the same magnitude, thus $F-5mg\mu=mg\mu$.

Is this idea correct?

Do you see that the entire system ( all three blocks ) begins to accelerate at $F > 3 \mu M g$?

 

[Lotto]

Do you see that the entire system ( all three blocks ) begins to accelerate at $F > 3 \mu M g$?

Yes. Is it in contradiction with my last post?

 

[erobz]

Yes. Is it in contradiction with my last post?

it’s not clear. Let me ask you what is the force of static friction acting between the stacked blocks up until that point?

 

[Lotto]

it’s not clear. Let me ask you what is the force of static friction acting between the stacked blocks up until that point?

Between the upper block and the middle block it is $mg\mu$, between the middle block and the bottom block it is $2mg\mu$. If I want to move with them, the inertial acceleration has to be bigger that $\frac{mg\mu}{m}=\frac{2mg\mu}{2m}=g\mu$. So if the inertial acceleration is $g \mu$, we can roughly say that it can start to move.

 

[erobz]

Between the upper block and the middle block it is $mg\mu$, between the middle block and the bottom block it is $2mg\mu$.

I think you are experiencing some common misconception. With $F \leq 3 \mu Mg$ the static friction force acting between the top block and middle block is zero, the static friction force acting between the middle block and lower block is also zero.

If I want to move with them, the inertial acceleration has to be bigger that $\frac{mg\mu}{m}=\frac{2mg\mu}{2m}=g\mu$. So if the inertial acceleration is $g \mu$, we can roughly say that it can start to move.

If you want to move them $F- 3 \mu M g > 0$, that will start the system moving. But until the acceleration exceeds $\mu g$ in this case they all move together. When the acceleration is greater than zero, but less than the value $\mu g$ the frictional forces acting on each block are whatever is required to maintain said acceleration of a particular block…nothing more, nothing less. If $\mu g$ is exceeded the blocks slip relative to the lower block.