What happens when you connect a charged capacitor to 2 uncharged capacitors?

[liam1992]

For my electronics work I have a question to answer:

"A 1000V source is used to fully charge a 1μF capacitor. The capacitor is then disconnected from the source and connected to two additional capacitors (2μF and 8μF) as shown in the circuit schematic below.

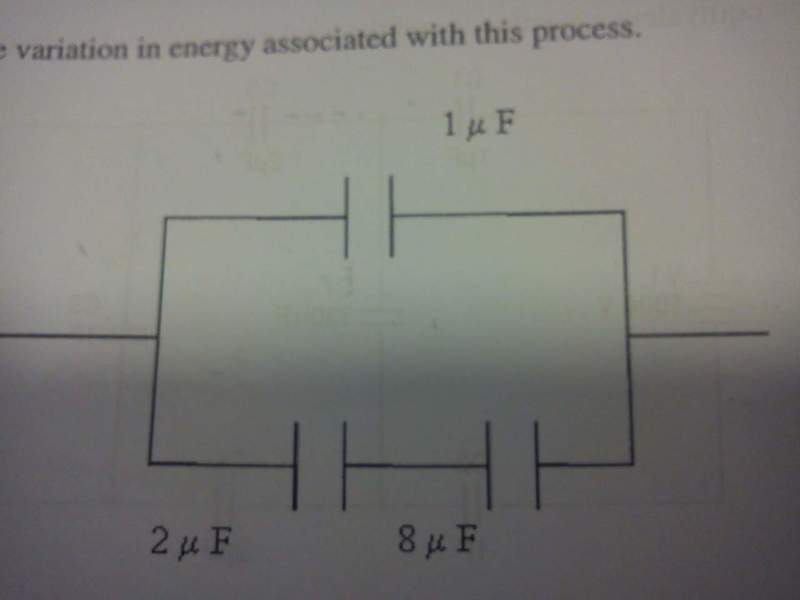
a) Calculate the final voltage across the 1μF capacitor after connecting it to the two capcitors.
b) Calculate the variation of energy associated with this process."

For the first part am I supposed to act as if the three capacitors are in parallel or what? And for the second bit what is the variation of energy? Any help would be greatly appreciated.

 

[tiny-tim]

hi liam1992!

For the first part am I supposed to act as if the three capacitors are in parallel or what? And for the second bit what is the variation of energy? Any help would be greatly appreciated.

you can do KVL round the loop (ie in series)

and once you've found the voltage across each capacitor, use the usual formula for the energy

 

[DragonPetter]

edit: I don't like my help (see: https://www.physicsforums.com/showthread.php?t=286555 )

 

[DragonPetter]

If you read this link: PDF, its shows why energy is not conserved, which is a pretty interesting fact that I think the problem is trying to expose you to.

The correct way to solve this problem is to solve for the voltage based on these two knowns:
1.) conservation of charge (the initial amount of charge in the charged capacitor will equal the number of charges distributed between the capacitors after discharging).
2.) KVL at steady state (when the capacitor has finished discharging into the uncharged capacitors), which implies the voltage across components in parallel are equal.

A first step is that you can combine the two uncharged capacitors in series as an equivalent capacitor. You now have 2 capacitors in parallel, where one is charged at 1000V and the other is uncharged.

Now, you know that the initial charge in the 1uF capacitor, q0, is equal to the sum of the final distributed charges between the 1uF capacitor, q1, and the equivalent uncharged capacitor, q2. So we can say:
$q_{0} = q_{1} + q_{2}$. This is based on the conservation of charge.

Next, since q = CV, we can say:
$C_{0}V_{0} = C_{1}V_{1} + C_{2}V_{2}$
Where the left hand side corresponds to the charged capacitor before discharging (1000V), and the right hand side corresponds to the charged capacitor and the other capacitor after the discharge.

But from our known that the voltage across the two capacitors must be the same after the discharge, we can say $V_{1} = V_{2} = V$. Now you just solve for V.


Like tiny-tim said, the energy can be calculated from the energy in a capacitor formula. Like the link I provded shows, you will see that the total energy has changed.

 

[rude man]

If you're going to do KVL or KCL you need to put an impedance between the 1 μF and the other two. The important point is to realize that some level of inductance and resistance (I dismiss the bit about superconductors occasionally mentioned) must obtain between the charged capacitor and the two uncharged ones.

 

[technician]

Calculating the charge and energy stored on the original 1uF capacitor is straight forward I hope.
The 8uF and 2uF capacitors are in series so their equivalent capacitance can be found.
The 1uF capacitor is connected in parallel with the 8uF,2uF combination so you should be able to find the total capacitance when the connection is made.
The total charge is constant and therefore you should be able to get the voltage across the combination... that is the voltage across 1uF.
The final energy stored can be found and it will be less than the original stored.
Energy is 'lost' when capacitors charge and discharge.