What is magnitude of dynamic force?

[Mech_LS24]

Summary:: In a mass-spring system they talk about 'magnitude of dynamic force', what is meant with that?

Hi!

In a mass-spring system I read about the term: "magnitude of dynamic force" (see sketch). What is meant with that? I the end this is used to determine the accuracy as I understand it now.

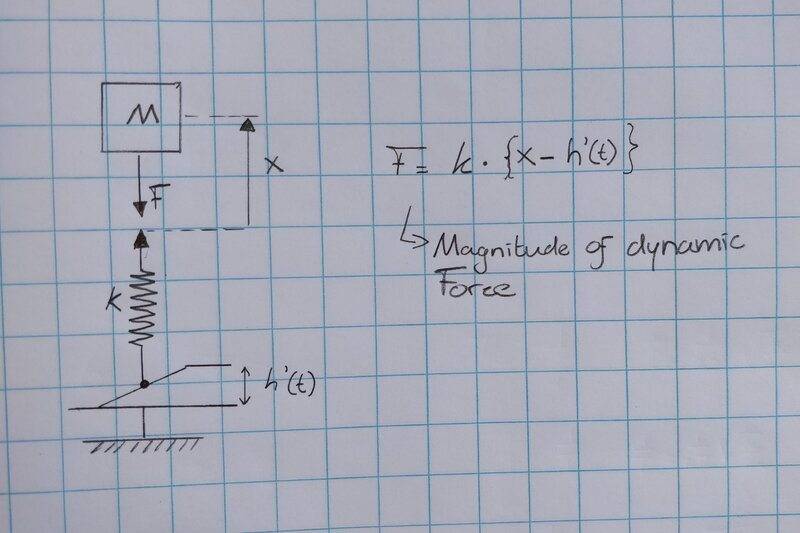
Thanks!

 

[jrmichler]

Is this a homework problem?

It appears that the wedge makes a sudden change to the position of the end of the spring, and you want to find the force between the spring and mass. It helps if you fully specify the problem, and say so. If so, make two hand sketches of that force vs time - one with the wedge inserted VERY slowly, and the other with the wedge inserted very fast. Does the mass bounce with one case and not the other case? Discuss, and we can help clear up any confusion.

 

[Mech_LS24]

Hi thanks for helping me :).

It isn't homework, just a section out a book where I am interested in, but I can't follow what they are saying here. The statement is that we should be interested in dynamic forces because in general they will cause wear and consequently limit the service life.

It is more or less my question on what that formula is based on?

Could you elaborate a bit more on the two hand sketches of force vs time? Do you mean something like this:

 

[jrmichler]

This is more like homework, so I moved it to the physics homework forum.

The formulas are easier to understand when you can visualize what happens in a spring mass system. Try an experiment. Hang a weight from a rubber band. The weight should be heavy enough to stretch the rubber band to 1.5 to 3 times its length. Hold the free end of the rubber band and move it up and down both slowly and fast. Make a fast vertical move, then hold still. Experiment. Observe the motion of the weight, and the effect on the length of the rubber band.

Since the force is proportional to the length of the rubber band, you should be able to make some qualitative sketches showing the input (your hand movement) and the output (length of the rubber band) as a pair of lines on the same axes.

 

[Mech_LS24]

Apologies for the misplacement.

I indeed have done some experiments, with a extension spring and a weight on it. I do understand what's happening, but can't relate it to the formulas. So when I move my hand slowly the weight is following the movement, when I move my hand faster the weight is going to extend and compress, when I even move it faster the weight is just hanging there. What can I sketch from that? I am really struggling with this, as I do understand the concept...

"Since the force is proportional to the length of the rubber band"

What do you mean with proportional?

 

[haruspex]

It is not at all clear to me what the diagram represents. Is there any description that goes with it?
It does appear to be a generalisation of forced oscillations, i.e. where the forcing function may be aperiodic. Reading about forced oscillations would be a good start, though.

 

[haruspex]

What do you mean with proportional?

In an ideal spring, which a rubber band is not, the force (compression or tension) is proportional to the change in length from its relaxed length. That is, if you double the length change then the force doubles.

 

[Mech_LS24]

In the end it is about how the output movement varies as a function of time when an input movement is applied, in other words, to determine the response. The behaviour of the output movement (x) differs from the behavior of the input movement (h'(t)). So how great is the difference between output and input movement u= x-h'(t).

The book gives two equations:
F = m*a = m*Ẍ
F = c*(x-h'(t) --> c is k

Is this want you meant with the sketch?:

 

[haruspex]

In the end it is about how the output movement varies as a function of time when an input movement is applied, in other words, to determine the response. The behaviour of the output movement (x) differs from the behavior of the input movement (h'(t)). So how great is the difference between output and input movement u= x-h'(t).

The book gives two equations:
F = m*a = m*Ẍ
F = c*(x-h'(t) --> c is k

Is this want you meant with the sketch?:
View attachment 297053

Ok, that all makes sense.
So do you still have a question?

 

[Mech_LS24]

Ok, thanks.