What Is Poynting's Vector and How Is It Calculated?

[Jack_O]

Problem:

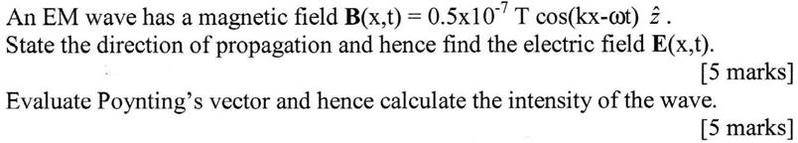
Attempt:

I think I've done the first bit correctly (but I'm not certain). As for the second half of the question I'm at a loss. I have looked up poyntings vector and found S=ExH where H is the auxiliary magnetic field (i'm not sure what this means) and S=(1/u(0)) (ExB), but I'm not sure what to do with it.

Any help appreciated.

 

[naresh]

In free space, the auxiliary field H is just $$B/\mu_0$$

Your answer to the first part is correct for the most part, however it is better to leave your final answer as a vector - that will help you evaluate vector cross products better. Please also check your integration step.

Wikipedia has an excellent article on the Poynting vectors, and how it is related to the intensity of the wave. You should look it up.
http://en.wikipedia.org/wiki/Poynting_vector