SUMMARY
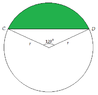
The discussion focuses on calculating the area of a segment bounded by a chord and an arc in a circle, specifically for chord $$\overline{CD}$$ measuring $$12\sqrt{3}$$ and subtending an angle of $$120^{\circ}$$. Participants utilize the law of cosines to determine the radius, which is found to be $$12$$. The area of the segment is derived by subtracting the area of triangle $$\triangle OCD$$ from the area of the sector formed by the angle. The triangle's area is calculated using the formula $$\frac{1}{2}bh$$, with the challenge of determining the height from the center of the circle.
PREREQUISITES
- Understanding of circle geometry and properties
- Familiarity with the law of cosines
- Knowledge of area calculation for triangles and sectors
- Basic trigonometry, including sine and cosine functions
NEXT STEPS
- Study the law of cosines for triangle side length calculations
- Learn how to calculate the area of a sector in a circle
- Explore methods for finding the height of a triangle using trigonometric ratios
- Practice problems involving segments and sectors of circles
USEFUL FOR
Students and educators in geometry, mathematicians interested in circle properties, and anyone seeking to understand area calculations involving circular segments.