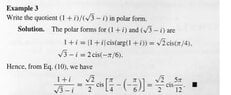What is the correct way to convert to polar form?

[nacho-man]

I started of with attempting to convert the numerator first

$ | 1 + i | = \sqrt{1^2+i^2}$
$= \sqrt{1-1} = 0$ ? this is wrong obviously, i don't see why its $\sqrt{2}$

for the second part

$ |\sqrt{3} - i|= \sqrt{3+1} = 2$

$ x = r \cos\theta$ $ y = r\sin\theta$

$x = 2\cos\theta$ $ y=2\sin\theta$

then $\theta = \frac{\pi}{3} and \frac{\pi}{6}$

$ = 2(\cos\frac{\pi}{3} + \sin\frac{\pi}{6} = 2cis(\frac{\pi}{3})$ I don't see why this is wrong either

 

[Ackbach]

The magnitude of a complex number $a+bi$ is given by $|a+bi|= \sqrt{(a+bi)(a-bi)}$. That is, you multiply a number by its complex conjugate, and then you take the square root.

 

[alyafey22]

$$1+i = \sqrt{2} \left( \frac{1}{\sqrt{2}}+i \frac{1}{\sqrt{2}}\right) = \sqrt{2} \, \text{cis} \left( \frac{\pi}{4} \right)$$

$$\sqrt{3}-i = 2 \left(\frac{\sqrt{3}}{2}- i \frac{1}{2} \right) = 2 \text{cis}\left( \frac{-\pi}{6}\right)$$

 

[nacho-man]

$\cos\theta = \frac{1}{\sqrt{2}}$
Therefore
$ \theta = \frac{\pi}{4}$
and $\sin\theta=\frac{-1}{\sqrt{2}}$
therefore
$\theta = \frac{\pi}{4} + \pi = \frac{5\pi}{4}$
What have i done wrong for the $\sin\theta$ part?

 

[Prove It]

The range of \displaystyle \begin{align*} y = \arcsin{(x)} \end{align*} is \displaystyle \begin{align*} \left[ -\frac{\pi}{2} , \frac{\pi}{2} \right] \end{align*}.