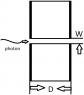
What is the Cutoff Wavelength for a Photon Passing Through a Waveguide?

[henxan]

Photon through a "wave guide"

Given the attached image.

A photon approaches a "slit/waveguide" of width W. The waveguide has a length D>\lambda...

What is the largest wavelength the photon can have, and still pass through?

 

[Born2bwire]

If you are talking photons, then pretty much any. With quantum mechanics you should find that there would be a non-zero, however incredibly small it would be, probability for the photon to traverse the waveguide. It's all just a question of where you want to specify the cut-off (1%, 0.1%, age of the Universe?).

For classical electromagnetics, it can also be a question of where you want to cutoff. In terms of propagating modes, that is a distinct answer. If you have a rectangular waveguide, then the cutoff wavelength for the lowest mode, assuming a square waveguide, is

\lambda_c = 2W

for the TE_{01} and TE_{10} modes.

But again, if you have a wavelength longer than the cutoff wavelength above, the wave will travel in attenuation. If the length of the waveguide is very short, then you can still get an appreciable amount of power transmitted through. So for the evanescent modes, it is once again just a question of what cutoff you wish to define in terms of the power reduction before you decide that the wave is effectively gone.

 

[henxan]

Thanks for answering! :)..

Yes, that was partially what I was wondering about, the cutoff wavelength :)..