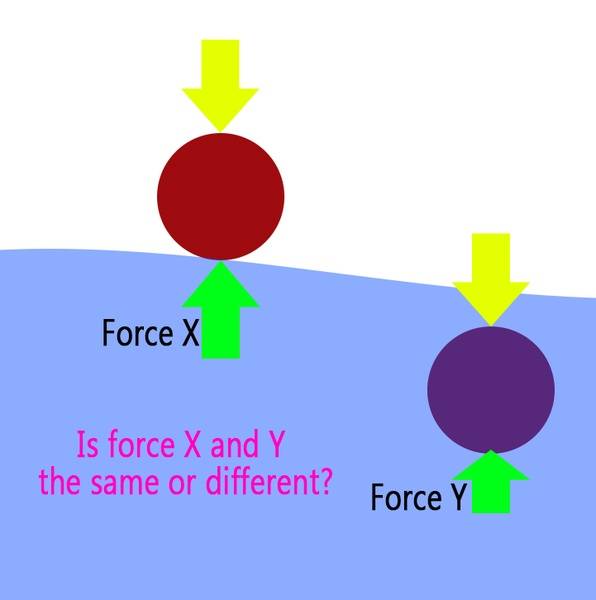
Discussion Overview
The discussion revolves around the differences between the force experienced during the initial impact with water and the force due to water resistance. Participants explore the physics of these forces, including the effects of shape, velocity, and the dynamics of deceleration upon entering the water.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants note that the force at first contact is different from the force due to water resistance, as the submerged object interacts with more water and transfers more momentum.
- There is a discussion about how the shape of the object (sphere vs. cube) may affect the resistance force compared to the force at first contact, particularly if the velocity is the same.
- One participant emphasizes the rapid, non-uniform deceleration experienced by the object as it enters the water, which leads to different internal stress forces on the object.
- Concerns are raised about the energy required to create a splash and the force needed to break the surface tension of the water, with some arguing that simple linear equations may not adequately describe the situation.
- Another participant introduces the concept of shock Hugoniot equations to explain the transient nature of impact pressure versus the steady-state pressure while submerged.
- There is a mention of how the momentum of the falling object contributes to the energy of the splash, and the distinction between displacement of water being velocity independent while the force of impact is not.
- Some participants highlight the importance of considering the time scale of the impact and the density of the object when discussing forces involved.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the differences between the forces, with multiple competing views and interpretations of the physics involved remaining present throughout the discussion.
Contextual Notes
Participants express uncertainty regarding definitions of terms like "resistance force" and the impact of various factors such as object shape, velocity, and the nature of the splash. There are also unresolved mathematical considerations related to the forces discussed.