What Is the Electric Field of a Curved Rod at the Origin?

[Zack K]

Homework Statement

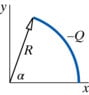
A rod of charged -Q is curved from the x-axis to angle $\alpha$. The rod is a distance R from the origin (I will have a picture uploaded). What is the electric field of the charge in terms of it's x and y components at the origin? k is $\frac {1} {4\pi \epsilon_0}$

Homework Equations

$\vec E=\frac {kQ} {r^2}$

The Attempt at a Solution

Let $\theta$ represent a any angle of $\alpha$
$\vec r=\langle -Rcos\theta, -Rsin\theta, 0\rangle$
$|\vec r|=\sqrt {(-Rcos\theta)^2+(-Rsin\theta)^2}$

$$\hat r=\frac {\vec r} {\vec |r|}=\frac {\langle-cos\theta, -sin\theta, 0\rangle} {\sqrt{-cos\theta)^2+(-sin\theta)^2}}=\frac {\langle-cos\theta, -sin\theta, 0\rangle}{1}$$You can factor out the R from the top and bottom and cancel them out. The denominator just becomes 1

Now representing $\Delta Q$
$$\Delta Q=Q\frac{\Delta arclength} {arclength}=Q\frac{R\Delta\theta} {R\alpha}=Q\frac{\Delta\theta} {\alpha}$$
The R's will cancel out.
Now assuming rod consists of many point charges
$$\Delta {\vec E}=\frac {k\Delta Q}{|\vec r|^2} \hat r=\frac {kQ\Delta \theta}{R^2\alpha}\langle-cos\theta, -sin\theta, 0\rangle$$Now we integrate in terms of $\theta$ and integrate each component. $$\Delta {\vec E_x}=\int_{0}^{\alpha} \frac {kQ(-cos\theta)}{R^2\alpha}d\theta=\frac {kQ}{R^2}\int_{0}^{\alpha} \frac {(-cos\theta)}{\alpha}d\theta$$ $$\Delta {\vec E_y}=\int_{0}^{\alpha} \frac {kQ(-sin\theta)}{R^2\alpha}d\theta=\frac {kQ}{R^2}\int_{0}^{\alpha} \frac {(-sin\theta)}{\alpha}d\theta$$This is where I'm stuck on. Not entirely sure if I can factor an alpha out.

 

[kuruman]

This is where I'm stuck on. Not entirely sure if I can factor an alpha out.

Why not? You are integrating over $\theta$ not $\alpha$ which is a given of the problem and which you may assume is constant. This will allow you to find the x and y components as functions of $\alpha$. You can test your work by seeing if you get the expected direction for $\alpha = \pi/2, \pi, 3\pi/2$.

 

[Zack K]

Why not? It is a given of the problem so you may assume it is constant. This will allow you to find the x and y components as functions of $\alpha$. You can test your work by seeing if you get the expected result for $\alpha = \pi/2, \pi, 3\pi/2$.

The problem I see is that for the x component when I integrate -cos it becomes -sin. But then if I put -sin(0) I would get 0 electric field on the x-axis which doesn't make sense.

 

[kuruman]

The problem I see is that for the x component when I integrate -cos it becomes -sin. But then if I put -sin(0) I would get 0 electric field on the x-axis which doesn't make sense.

When you integrate the trig function, you get $-\sin \theta |_0^{\alpha}$. What does that give you?

 

[Zack K]

When you integrate the trig function, you get $-\sin \theta |_0^{\alpha}$. What does that give you?

$-sin\alpha$ but, wouldn't this mean that I have no variables in my function then? All I would have are constants.

 

[kuruman]

$-sin\alpha$ but, wouldn't this mean that I have no variables in my function then? All I would have are constants.

Your variables are $Q$, $\alpha$ and $R$. You are calculating $E_x$ and $E_y$ if $Q$, $\alpha$ and $R$ are given to you. What else is there to be said?

 

[Zack K]

Your variables are $Q$, $\alpha$ and $R$. You are calculating $E_x$ and $E_y$ if $Q$, $\alpha$ and $R$ are given to you. What else is there to be said?

But the equation let's say for $\vec E_x=\frac {kQ(-sin\alpha)}{R^2\alpha}$ doesn't seem like it holds. I don't see any variables, alpha is a constant. Even if I treated it as a variable, and wanted to find $\vec E_x$ at $\alpha=0$ Then I would get sin(0) which is 0 and isn't true in this case(I uploaded a diagram). Not to mention how you would have a 0 on the denominator.

 

[Hiero]

Homework Equations

$\vec E=\frac {kQ} {r^2}$

This is probably just a typo, but you cannot equate a (multi-dimensional) vector with a scalar

Now assuming rod consists of many point charges
$$\Delta {\vec E}=\frac {k\Delta Q}{|\vec r|^2} \hat r=\frac {kQ\Delta \theta}{R^2\alpha}\langle-cos\theta, -sin\theta, 0\rangle$$

Remember, the charge is given as negative Q.

But the equation let's say for $\vec E_x=\frac {kQ(-sin\alpha)}{R^2\alpha}$ doesn't seem like it holds. I don't see any variables, alpha is a constant.

Perhaps you’re wondering why the field does not depend on x,y position? Remember, you’ve only calculated the field at a particular point! (At the origin.)

Even if I treated it as a variable, and wanted to find $\vec E_x$ at $\alpha=0$ Then I would get sin(0) which is 0 and isn't true in this case(I uploaded a diagram). Not to mention how you would have a 0 on the denominator.

0/0 is not necessarily zero. You have to take the limit. Doing so should give you Coulomb’s law for a point charge at (x,y) = (R,0) because that is the situation α=0 describes. (But again, you’ve only determined the field at a particular point.)

 

[kuruman]

Everything I had to say has already been covered by @Hiero in the preceding post. Just think about it.

 

[Zack K]

This is probably just a typo, but you cannot equate a (multi-dimensional) vector with a scalar

Yes sorry that was a typo.

Remember, the charge is given as negative Q.

That was a typo as well.

Perhaps you’re wondering why the field does not depend on x,y position? Remember, you’ve only calculated the field at a particular point! (At the origin.)

Ah I see I just realized that the equation is for the origin and is a constant value at the origin. There would be no reason to have a variable since the origin is fixed.

@kuruman
@Hiero
Thank you guys so much.