SUMMARY
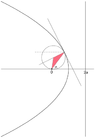
The equation of a circle that touches the parabola defined by the polar equation $2a/r=1+\cos(\theta)$ at the point $\theta=\alpha$ is derived using geometric properties and trigonometric identities. The polar representation of the circle is given by the formula $r\cos^3\left(\frac{1}{2}\alpha\right) = a\cos\left(\theta - \frac{3}{2}\alpha\right)$. The center of the circle is located at polar coordinates $(R, \frac{3}{2}\alpha)$, where $R = \frac{a}{2\cos^3(\alpha/2)}$. This analysis confirms that the tangents of both curves are parallel at the point of tangency.
PREREQUISITES
- Understanding of polar coordinates and their equations
- Knowledge of conic sections, specifically parabolas
- Familiarity with trigonometric identities and half-angle formulas
- Ability to differentiate functions in polar coordinates
NEXT STEPS
- Study the properties of conic sections in polar coordinates
- Learn about the derivation of polar equations for circles
- Explore the application of trigonometric identities in geometric proofs
- Investigate the relationship between tangents and curves in polar systems
USEFUL FOR
Mathematicians, physics students, and anyone interested in advanced geometry and the application of polar coordinates in conic sections.