What is the Equation on My T-Shirt?

[DelfinDelfin]

I have a t-shirt with a next print:

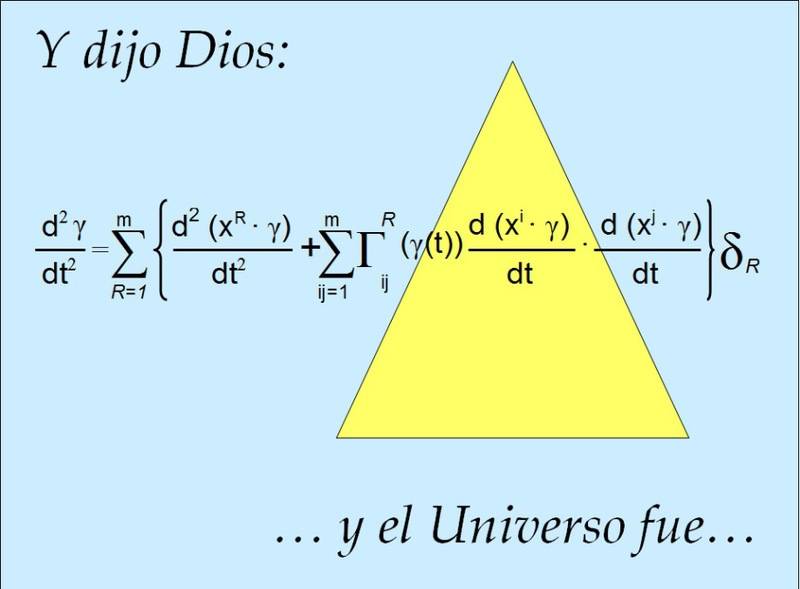
But I am not sure what equation is. I only know that is something related with light. But I haven't found it. I am not sure if it is one from quantum electrodynamics or some advanced course in physics. I would appreciate that somebody could tell me which one is

 

[Mapes]

I don't have much of a guess, but since nobody else has responded, I'll tell you that to a mechanical engineer, the general form looks similar to d'Alembert's[/PLAIN] principle (see equation 1 in that link) in mechanics in that you seem to have an infinitesimal displacement on the far right and an acceleration on the left-hand side. But more broadly, d'Alembert's principle is a variational approach (see, e.g., Fermat's[/PLAIN] principle, which is an example of variational methods applied to light propagation). Not much, but it might help your search.

 

[mfb]

The $\Gamma$ looks like a Christoffel symbol (although it should have two indices as superscripts and one as subscript), and the equation seems to be about general relativity.

 

[Orodruin]

The $\Gamma$ looks like a Christoffel symbol (although it should have two indices as superscripts and one as subscript), and the equation seems to be about general relativity.

The Christoffel symbols usually have two subscripts and one superscript, which the equation has.

 

[mfb]

All examples I found had it the opposite way. Maybe both ways are common. Well, just a matter of convention of course.

Edit: I got confused, ignore this post.

 

[Orodruin]

All examples I found had it the opposite way. Maybe both ways are common.

The Wikipedia page you link to has it the "normal" way. Two down and one up. I have never seen two up and one down.

 

[mfb]

Wait, I got confused. Yes, one up, two down. Ignore my previous post.

 

[Khashishi]

Something looks funny about that equation. It looks like there are dot products $x^R \cdot \gamma$. Which means that $x$ and $\gamma$ are tensors. But if that's the case, then what rank is $\gamma$? The rank of the LHS and RHS ought to be the same, but it doesn't seem possible. The second term in the curly brace seems to have a dot between the two derivatives, but this might just be a multiplication. All the dots might be simply multiplications. It's too bad that mathematical notation can be so ambiguous.

 

[DrGreg]

First, I think the $R$ really should be a $k$ and has been transcribed incorrectly.

I would guess this is supposed to be what, in more conventional tensor notation, would be written:

And God said:$$
\frac{D^2\gamma^k}{dt^2} = \frac{d^2\gamma^k}{dt^2} + \Gamma^k{}_{ij} \frac{d\gamma^i}{dt} \frac{d\gamma^j}{dt}
$$... and there was the Universe...*​

It expresses acceleration along a curve $\vec{\gamma}(t)$ in non-Cartesian coordinates, where $\vec{x}^k$ is the $k$th coordinate dual basis covector and so $\gamma^k = \vec{x}^k \cdot \vec{\gamma}$. But they seem to have messed it up and I can't work out why there's an extra $(\gamma(t))$ in the middle of it all. Presumably the $\delta_k$ is the basis vector too.

*Translation assisted by Google Translate

 

[jedishrfu]

I think its an artificially contrived equation designed to look cool similar to Japanese t-shirt logos with nonsense English.

But Dr Greg's explanation is quite plausible too.