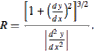Discussion Overview
The discussion revolves around determining the fastest speed an object can achieve while navigating a specific curve defined by the equation (0.0033x² - 1.0038x + 98.2331). Participants explore various factors affecting speed, including centripetal force, friction, and the geometry of the curve, while considering both theoretical and practical implications.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants assert that the centripetal force formula (mv²)/r applies primarily to circular motion, questioning its applicability to the given curve.
- Others argue that there is theoretically no upper limit on speed as long as the curve can withstand the necessary centripetal force and friction is not infinite.
- A participant mentions that at each point on the curve, there exists a maximum speed determined by the radius of curvature and static friction, suggesting a method to calculate slip speed.
- Some contributions highlight the distinction between orbital motion and contact force scenarios, emphasizing the need to consider the specific forces acting on the object.
- One participant proposes using energy conservation principles to analyze speed, suggesting that maximum speed occurs where potential energy is minimized.
- Another participant provides a method for locating the apex of the parabola to determine maximum curvature, which could influence speed calculations.
- Several posts reiterate the importance of friction and the forces available to the object, questioning how these factors influence the maximum speed achievable on the curve.
- A participant requests mathematical techniques for calculating the radius of curvature at various points along the curve without manual computation.
Areas of Agreement / Disagreement
Participants express differing views on the limits of speed around the curve, with some suggesting theoretical limits based on physical constraints while others argue for the absence of such limits. The discussion remains unresolved regarding the best approach to calculate maximum speed, with multiple perspectives presented.
Contextual Notes
Participants note that the analysis may depend on specific assumptions about forces, friction coefficients, and the nature of the curve. There are also references to the need for numerical methods to solve the problem if analytical solutions prove difficult.
Who May Find This Useful
This discussion may be of interest to those studying dynamics, vehicle performance, or mathematical modeling of curves in physics and engineering contexts.