Discussion Overview
The discussion revolves around the properties of parabolas, specifically focusing on the general equation of a parabola with a vertex not at the origin. Participants explore the implications of the parameters in the equation, the orientation of the parabola, and the relationship between the vertex, focus, and directrix.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
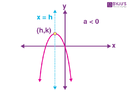
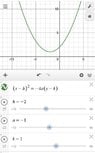
- Some participants present the general equation of a parabola as ##(x-h)^2=-4a(y-k)##, indicating it opens downwards with vertex at (h,k).
- Others argue that the sign of ##a## determines the direction the parabola opens, with ##a<0## suggesting it opens downwards and ##a>0## suggesting it opens upwards.
- A participant questions the validity of the equation when ##a<0##, asserting that it leads to contradictions regarding the signs of the left and right sides of the equation.
- There is a contention about the definition of the "general equation of a parabola," with some asserting that it varies based on the orientation (upward/downward vs. left/right).
- Participants discuss the significance of the parameter ##a##, noting it represents the distance from the vertex to the focus, and raise questions about how it can be both positive and negative.
- One participant attempts to clarify the relationship between the focus, directrix, and the parabola, providing examples based on the equation ##y=x^2##.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the definition of the general equation of a parabola, with multiple competing views on its forms and implications. The discussion remains unresolved regarding the correct interpretation of the parameters and their effects on the parabola's orientation.
Contextual Notes
There are limitations in the discussion regarding the assumptions made about the parameters and the definitions used for the equations. Some participants express confusion about the graphical representation of the equations and the implications of the variable ##a##.