- #1
rudransh verma
Gold Member
- 1,067
- 95
- TL;DR Summary
- Problem in general eqn of parabola
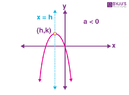
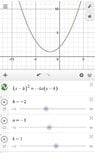
The general eqn of parabola is ##(x-h)^2=-4a(y-k)##. This is the parabola whose vertex doesn't lie on origin and axis is parallel to y axis. It opens downwards. Vertex is (h,k). What will be the focus of this parabola and what is ##a## in general form?
In the diagram a<0 which is confusing.https://byjus.com/maths/standard-equations-of-parabola/
In the diagram a<0 which is confusing.https://byjus.com/maths/standard-equations-of-parabola/