What is the governing equation of a spring with sinusoidal excitation?

[k.udhay]

TL;DR

Most of the spring vibration lectures assume spring to be fixed on one end and mass on the other end. In my case, spring has a sinusoidal excitation on one end and mass on other end. How to get the governing equation?

Hi,
Most of the spring vibration lectures assume spring to be fixed on one end and mass on the other end [Example]. In my case, spring has a sinusoidal excitation on one end and mass on other end. Pl. refer the image below.

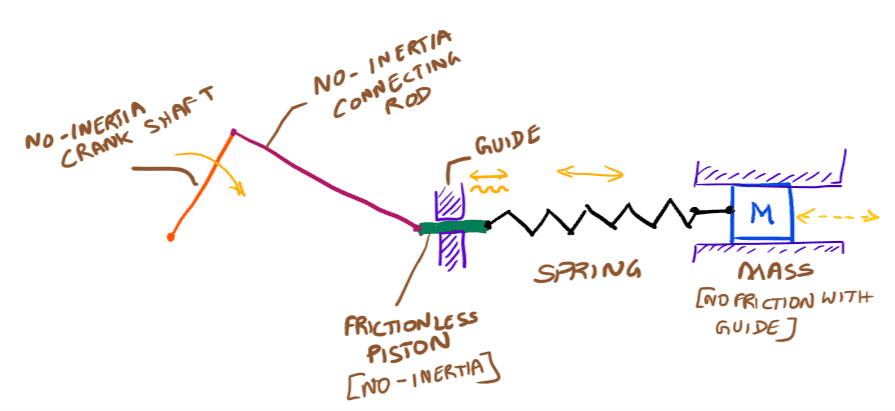
How to get the governing equation? With that I also want to find the resonance frequency of the system. To reduce complexity, I have not taken dampening into account. I will add it later. Pl. help.

 

[Dr.D]

The force in the spring is K*(deformation) where the deformation is the difference between the current length and the unstrained length. The slider-crank determine the location of the left end if the spring, and the right end is the current location of the mass. Its not a hard problem at all.

 

[k.udhay]

The force in the spring is K*(deformation) where the deformation is the difference between the current length and the unstrained length. The slider-crank determine the location of the left end if the spring, and the right end is the current location of the mass. Its not a hard problem at all.

Thank you Dr. Do you know any elaborate lecture or derivation available on the internet to understand further details?

 

[Dr.D]

No, I don't know of any such.

Are you given dimensions and a coordinate system? If not, you will need to assign some. Do you know the free length of the spring (length with no force in the spring)? This is neccasary because deformation is measured from this state.

 

[anorlunda]

Thank you Dr. Do you know any elaborate lecture or derivation available on the internet to understand further details?

One of the best lessons I learned in engineering school is the ability to derive my own equations to adapt to the actual problem. I wager that you already have all the fundamentals needed to derive your own equations for this problem. You should try. Try hard.

Courses sometimes fail to mention that derivation skills are as important as solving skills.

 

[k.udhay]

No, I don't know of any such.

Are you given dimensions and a coordinate system? If not, you will need to assign some. Do you know the free length of the spring (length with no force in the spring)? This is neccasary because deformation is measured from this state.

I am more interested in the time dimension. As the speed of the crank changes, the acceleration input to the spring changes. At some speed(s) it is going to resonate. Hence, time is what is more a challenging parameter for me.

 

[Dr.D]

Most of this problem is in the kinematics. You cannot describe the kinematics as a function of time until you assign some time varying coordinates. If you need further help, I suggest you contact me by PM to discuss it.