SUMMARY
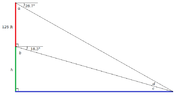
The height of the cliff in the given scenario is approximately 206.4 feet. This conclusion is derived from the application of the law of sines using the angles of depression from both the top and base of a 125-foot tower. The angles calculated are 61.3 degrees and 71.7 degrees, which are used to find the height of the cliff through trigonometric relationships. The calculations confirm that the cliff's height is significantly greater than initially estimated at 190.71 feet.
PREREQUISITES
- Understanding of basic trigonometry, specifically the law of sines.
- Familiarity with angles of depression and their application in real-world scenarios.
- Ability to interpret and create geometric diagrams based on word problems.
- Knowledge of how to calculate heights using trigonometric functions.
NEXT STEPS
- Study the law of sines in-depth to understand its applications in various geometric problems.
- Practice solving problems involving angles of depression and elevation.
- Learn how to accurately create and interpret geometric diagrams for complex scenarios.
- Explore advanced trigonometric concepts such as the law of cosines for additional problem-solving techniques.
USEFUL FOR
Students, educators, and professionals in fields requiring mathematical problem-solving skills, particularly in geometry and trigonometry, will benefit from this discussion.