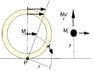
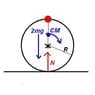
What Is the Instantaneous Axis of Rotation for a Pure Rolling Disc?

[kushan]

Homework Statement

if a disc of mas m is pure rolling , with velocity v .

the instantaneous axis of rotation would be the point of contact with the ground .
As shown in the diagram this could be considered as a disc rotating about one of the point on circumference for an instant of time .
Since this is circular motion , a centripetal force should exist .
hence
mg=mv^2/r
this gives us a limiting value of velocity .
Please correct me with this ambiguity .
Thank you

 

[voko]

The acceleration is not due to gravity. It is due to the reaction of the spokes in the wheel. Gravity does help somewhat, but not significantly. Consider the velocity of 10 m/s. It is well within the typical urban speed limits. For a typical 0.25 m radius wheel, the acceleration would be 40 g, so the acceleration due to gravity is negligible.

 

[kushan]

but according to equation which i deduced , give me if velocity is greater than root of gr ball will bounce up

 

[voko]

Please re-read my example. Do you really think that cars going at 10 m/s bounce up?

 

[kushan]

but according to the equation it should bounce.
But it doesn't right ?
why

 

[voko]

I have personally driven cars at about 70 m/s. That gives about 1.5 THOUSAND g for the wheel. And believe me, the cars did not lose traction at those speeds.

As to why, I did explain: the acceleration is due to the tension in the wheel spokes, not gravity.

 

[kushan]

Ok tell me if I somehow , exceed root gr will it bounce up

 

[voko]

I have explained the physical reason and have provided examples of real motion that violates your conjecture. I do not see what else I can do.

 

[kushan]

Can anyone else explain this ?

 

[ehild]

Can anyone else explain this ?

Kushan,

When a point mass does not experience enough force for a circular motion it will leave the circle along its tangent.
You say that gravity is not enough to drive the CM along the circle of radius r around the instantaneous axis. What happens with the CM then? It will not rise. It will move along the horizontal tangent.
But that is what the CM does during rolling: Moves along a horizontal straight line at distance r above the ground.
When you try to treat rolling using the instantaneous axis you can fall into traps. Do not forget that the instantaneous axis is fiction. It travels, and it does not belong to the rolling body.
It is more clear to consider the in-plane motion of rigid bodies as a traveling motion of the CM and rotation about the CM.


ehild

 

[kushan]

Ehild , I almost forgot that body doesn't fly off it moves tangentially . Thanks for reminding me .
So, you mean to say if gravity isn't sufficient enough the body will fly off tangent , and that is horizontal to ground . Okey I get it .
But there's a question in my textbook which precisely asks when will the system jump off , here it is "
A ring of mass m is rolling on a plane surface (assume friction is sufficient enough to support pure rolling ) , with a small particle of mass m permanently attached to its rim .
At some moment this mass reaches the base and at this instant the center of ring moves with velocity v .
At what values of v will the ring move without bouncing .
"
In this question the moment system tends to bounce it will be brought back to rolling , because after leaving the ground system will move tangent to its initial velocity .

 

[ehild]

If there is some extra mass on the rim the CM will not be at the centre of the ring. The centre of the ring moves horizontally, but the CM rotates about it. It moves along a circle of radius determined by the ratio of the small mass to the mass of the ring. Was the mass ratio given?

ehild

 

[kushan]

Mass ratio is 1 , or both have same masses

 

[ehild]

In a frame of reference moving horizontally with velocity v, the CM performs circular motion about the centre of the wheel. The radius of that circle is r=R/2.
The CM moves under the effect of the external forces, as if the resultant force acted at the CM. The resultant force is N-2mg.
If the red mas is at the bottom of the wheel the centripetal force has to point upward, N -2mg =2mrω². That can be fulfilled with every value of ω, as the only restriction for the normal force N is that it points upward.
Bouncing occurs when N needs to be equal or less then zero in order to maintain the circular motion. That can happen when the red mass is on the top of the wheel, the CM is above the centre of the wheel and the centripetal force has to point downward.

Find the maximum v.

ehild

 

[kushan]

Ehild ,
Can you please explain further why centripetal force would be max at top ,
I deduced an equation which give velocity minimum at top .
And centripetal force is proportional to velocity .

 

[ehild]

The velocity of the centre of the wheel is given: v. That determines the centripetal force which keeps the CM moving along its circle. It is the same both at top and bottom. The centripetal force is the resultant of gravity and the normal force. Bouncing can happen if the ground can not produce the necessary normal force.

ehild

 

[kushan]

Does that mean the velocity of center of mass remains v throughout ?

 

[ehild]

I might misunderstand the problem. What does it mean that the wheel moves without bouncing? If v is the speed of the centre when the mass on the rim is at the bottom, the potential energy is minimum. If the wheel turns over, the potential energy increases by 2mgr, and the kinetic energy has to cover it.
Can you copy the exact text?

ehild

 

[kushan]

ok I make a new thread , regarding this post