What is the intersection point of two objects on a position vs time graph?

[nmnna]

Homework Statement

Given a position vs time graph.
1)Find $\frac{v_{2}}{v_{1}}$
2)At what time the objects will meet?
3)Find $\frac{\Delta{x_2}}{\Delta{x_1}}$, if the second object started moving from the origin.

Relevant Equations

$v = \frac{\Delta{x}}{t}$

The graph:

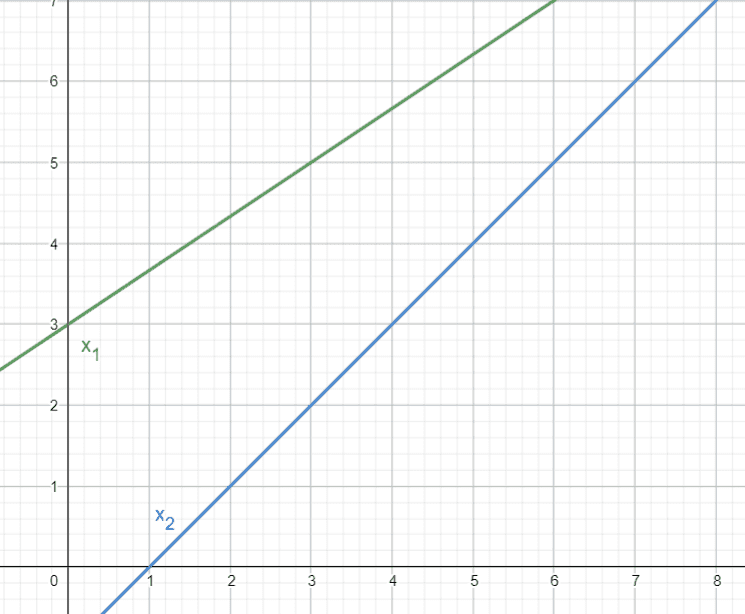
1) $$v_1 = \frac{\Delta{x}}{t} = \frac{5 - 3}{3} = \frac{2}{3}$$
$$2 = \frac{\Delta{x}}{t} = \frac{4 - 0}{5 - 1} = 1$$
$$\frac{v_2}{v_1} = \frac{1}{2/3} = \frac{3}{2} = 1.5$$

2)Points of intersection of the lines with the x-axis: $I$ (0; 3) and $II$ (0; -1), thus
$$\frac{2}{3}t + 3 = t - 1$$
$$t=\frac{-4}{(\frac{2}{3} - 1)} = 12 \ \text{seconds after starting motion}$$

I'm confused about the 3rd part.
If the second object starts moving from the origin then the graph should look something like this

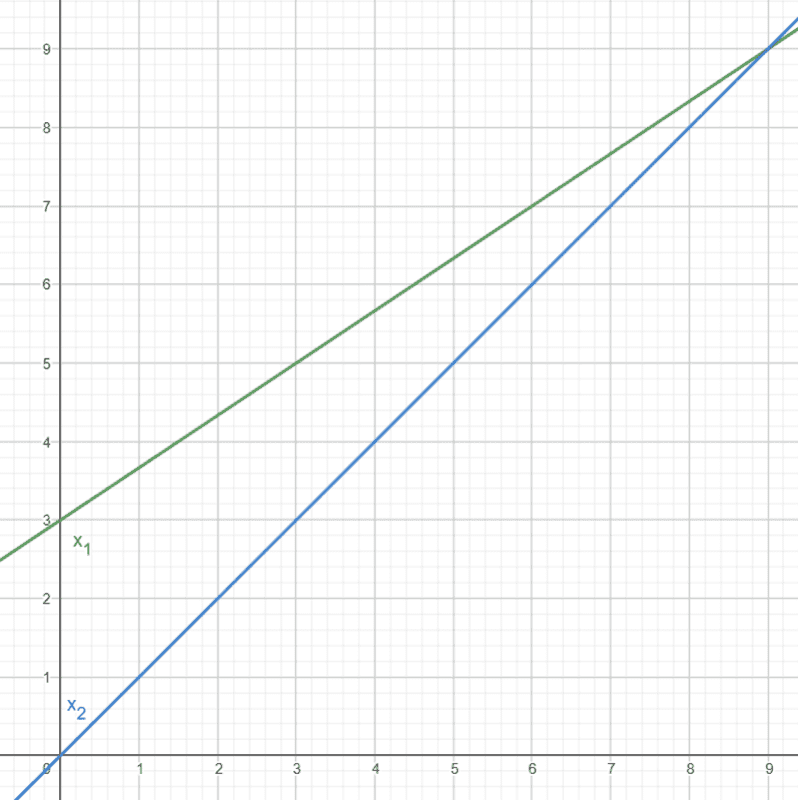
We can clearly see that the objects met when 9 seconds passed and calculations lead to the same value as well:
$$\frac{2}{3}t + 3 = t$$
We know that the velocity of the first one is $\frac{2}{3} \frac{\text{m}}{\text{sec}}$, we can find the distance it passed in 9 seconds, which is $6$ meters, for the second one I got $9$ meters. So the ratio $\frac{\Delta{x_2}}{\Delta{x_2}} = \frac{9}{6} = 1.5$.
But the answer in my textbook is 1.375
Where I went wrong?
This is a translation from another language so if something is not clear please tell me.

 

[BvU]

I'm confused about the 3rd part.

So am I . The only explanation I can give that comes out at the book answer is:
3) Assume the point of intersection is the same as in part 2 -- but object 2 started from the origin.

$\$

 

[nmnna]

So am I . The only explanation I can give that comes out at the book answer is:
3) Assume the point of intersection is the same as in part 2 -- but object 2 started from the origin.

I thought about this situation too, but by solving this i got $\frac{12}{2/3\times12+3} = \frac{12}{11} \approx 1.09$, which is not the expected answer...

 

[BvU]

What is the position of the intersection point in 2) ?

$\$

 

[nmnna]

What is the position of the intersection point in 2) ?

$\$

 

[TSny]

You can get their answer if you assume that object 2 starts at the position of the origin of the x-axis. (Don't change the original graph for object 2.) Assume object 1 starts at x = 3. The problem should have explicitly stated this if this is what they intended. With this interpretation, the two objects do not start their motions at the same time.

 

[nmnna]

You can get their answer if you assume that object 2 starts at the position of the origin of the x-axis. (Don't change the original graph for object 2.) Assume object 1 starts at x = 3. The problems should have explicitly stated this if this is what they intended. With this interpretation, the two objects do not start their motions at the same time.

As I understand from your answer my solution should look something like this, right?
$$\frac{\Delta{x_2}}{\Delta{x_1}} = \frac{(2/3\times12) + 3}{(9\times1) - 1} = \frac{11}{8}$$
[edit] This is wrong

 

[mrphysics]

I think in order to get the answer you want, you have to consider that the objects will meet at t=12sec. but the second object will have a different velocity. In that case you get : 11/8=1.375. The velocity of the second object has to be 11/12 so that : 12*(11/12)=11=(2/3)*12+3.

 

[TSny]

As I understand from your answer my solution should look something like this, right?
$$\frac{\Delta{x_2}}{\Delta{x_1}} = \frac{(2/3\times12) + 3}{(9\times1) - 1} = \frac{11}{8}$$
PS This is wrong

I don't understand your calculation. The numerator appears to be calculating the position of object 1 at t = 12, but you're using this for $\Delta x_2$.

One way to interpret part 3 is to assume that the brown dots represent the starting points of the two objects.

 

[hmmm27]

As noted by BVU in the second post in this thread, the book answer for part 3 is correct if (as stated) the 2nd object's line is changed to go through (0,0), and also the original intersection between the objects' lines (12,11) stays the same.

 

[BvU]

As shown below: green has done 8, red has done 11.

$\$