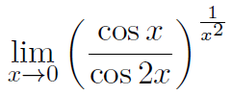SUMMARY
The limit of the function \(\lim_{x\to 0}\left(\frac{\cos(x)}{\cos(2x)}\right)^{1/x^2}\) evaluates to \(e^{3/2}\) using Maclaurin series expansion. The series expansions for \(\cos(x)\) and \(\frac{1}{1-x}\) are utilized to derive the limit without applying L'Hospital's Rule. The transformation of the limit into the form \(\lim_{n\to\infty} (1+\frac{3/2}{n})^n\) confirms the result through the definition of the exponential function. This approach emphasizes the power of series expansions in solving limits.
PREREQUISITES
- Understanding of Maclaurin series expansion
- Familiarity with limits and indeterminate forms
- Knowledge of exponential functions and their definitions
- Basic algebraic manipulation skills
NEXT STEPS
- Study the properties of Maclaurin series and their applications
- Learn about different types of indeterminate forms in calculus
- Explore the derivation and applications of the exponential function
- Investigate alternative methods for solving limits, including L'Hospital's Rule
USEFUL FOR
Students of calculus, mathematicians, and anyone interested in advanced limit evaluation techniques without relying on L'Hospital's Rule.