Homework Help Overview
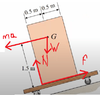
The discussion revolves around determining the maximum acceleration of a crate on an incline before it tips over. The problem involves concepts from mechanics, specifically relating to forces, torques, and friction on an inclined plane.
Discussion Character
Approaches and Questions Raised
- Participants explore the conditions for tipping over versus slipping, questioning the relationship between normal force, friction, and torque. There are attempts to derive equations related to forces and moments acting on the crate.
Discussion Status
Multiple interpretations of the problem are being explored, particularly the conditions under which the crate will tip versus when it will slip. Some participants have provided calculations for maximum acceleration, while others emphasize the need to clarify the conditions for tipping.
Contextual Notes
There is an ongoing discussion about the assumptions made regarding the point of action for forces and the relevance of torque in determining tipping conditions. Some participants express uncertainty about the definitions of slipping and tipping, indicating a need for further exploration of these concepts.