What is the maximum induced EMF in a rotating contour near a straight wire?

[Ivan Antunovic]

I have one more question , suppose we weren't using derivatives to find our angle θ for maximum emf induced, because it takes too much time ,
when θ = 0 and since cosθ , the magnetic flux will be maximum , emf induced is derivative of magnetic flux so it is connected with sinθ and sinθ is maximum for π/2.

I think that Force should be in the direction as shown on the picture

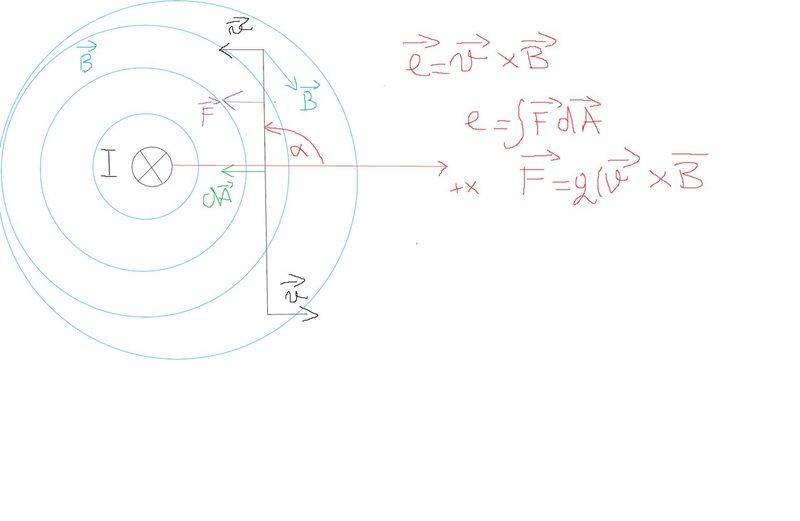
image sharing

by definition
F = q(v x B), and e = integral ( (vxB) * dA) )
I can't find cross product of v x B with right hand rule since they are not making angle of 90 degrees,
and I should use matrix calculations to find it but that again involves a lot of math ,
but both F and dA should make angle of 0 degrees to get our maximum emf induced,
so that we get cos(0) = 1 , and therefore e = F*A *cos(0) = F*A , where we get our maximum induced emf.
Is my thinking legit?

 

[TSny]

I think that Force should be in the direction as shown on the picture

The cross product v x B produces a vector that is perpendicular to the plane containing v and B.

F = q(v x B), and e = integral ( (vxB) * dA) )

The integral should not be an integral over a surface. It should be an integral along a line.

I can't find cross product of v x B with right hand rule since they are not making angle of 90 degrees,
and I should use matrix calculations to find it but that again involves a lot of math

You'll need to decide which sides of the square contribute to the emf. Once you do that, it will not be too difficult to find the angle between v and B for the sides that contribute. You will not need to use a matrix to find the cross product.

but both F and dA should make angle of 0 degrees to get our maximum emf induced,
so that we get cos(0) = 1 , and therefore e = F*A *cos(0) = F*A , where we get our maximum induced emf.
Is my thinking legit?

Force times area does not have the dimensions of emf. Area will not be relevant here.

Edit: Also, it might make the geometry a little easier to have the current coming out of the page in your previous picture. Then the angle between v and B will be less than 90^o.

 

[Ivan Antunovic]

The cross product v x B produces a vector that is perpendicular to the plane containing v and B.The integral should not be an integral over a surface. It should be an integral along a line.

You'll need to decide which sides of the square contribute to the emf. Once you do that, it will not be too difficult to find the angle between v and B for the sides that contribute. You will not need to use a matrix to find the cross product.Force times area does not have the dimensions of emf. Area will not be relevant here.

Edit: Also, it might make the geometry a little easier to have the current coming out of the page in your previous picture. Then the angle between v and B will be less than 90^o.

Sorry for the late replay.
it's e = 1 /q closed loop integral ( F dS), I tried to draw some positions of my contour and as my angle goes from 90 - 180, angle between v and B becomes greater and then their vector product becomes less.After 180 degrees emf gets negative and becomes minimum at angle -270 degrees , that is what I see from my drawings. Also the force is coming out of the board as you said? Well I am so stupid because of thinking that force should be in the direction of v.

image hosting no register

 

[TSny]

You will need to consider each of the 4 sides of the loop separately. For example, the figure below shows looking down on the top side of the loop, similar to your picture. The green dots show arbitrary points on the top side. As you see, the direction of v x B is out of the page or into the page. Therefore, is any emf developed along this side?

Next consider one of the sides of the loop that is parallel to the current.

 

[Ivan Antunovic]

You will need to consider each of the 4 sides of the loop separately. For example, the figure below shows looking down on the top side of the loop, similar to your picture. The green dots show arbitrary points on the top side. As you see, the direction of v x B is out of the page or into the page. Therefore, is any emf developed along this side?

Next consider one of the sides of the loop that is parallel to the current.

If I am right ,at the top green dot the direction of v x B direction is into the board , and at the bottom green line the v x B product is out of the board , and the angle between v x B is the same both on top and bottom green dot , therefore emf of the same magnitude will be produced just opposite direction ?

 

[TSny]

There is no emf generated in the loop at either green dot.

In order for v x B to produce a nonzero emf in an element of length of the circuit, v x B must have a component parallel to the element of length. The emf of the entire loop is the integral of (v x B)$\cdot$ dl around the loop. For which sides of the loop is the dot product of (v x B) and dl nonzero?

 

[Ivan Antunovic]

There is no emf generated in the loop at either green dot.

In order for v x B to produce a nonzero emf in an element of length of the circuit, v x B must have a component parallel to the element of length. The emf of the entire loop is the integral of (v x B)$\cdot$ dl around the loop. For which sides of the loop is the dot product of (v x B) and dl nonzero?

Okay I just changed view a little bit , because I couldn't figure it out other way.

upload pic

Case one is when α = 0 ° , where I get e = 0 , which is very intuitive.
Case two is when α = 90 °, and since part 3 and 4 of contour don't contribute to the emf induced , I am only left with part 2 and 1 , and there (v x B) make angles 0 °and 180° , making it maximum. That way your idea?

 

[TSny]

OK, but for sides 1 and 2 isn't v x B opposite to dl for both of these sides?

 

[Ivan Antunovic]

OK, but for sides 1 and 2 isn't v x B opposite to dl for both of these sides?

Yes you are right for side 2 I took v from part 1 in my v x B.

One big thank you, sir @TSny !

After this conclusion , I am trying to derive to maximum emf induced with new approach , my first approach takes too much time (finding magnetic flux , taking derivative of flux as a function of time) , tried to find e1 , and since e max= 2 *e1 it's much easier to find the maximum emf induced, but messed something up with my integral after substitution for dl

EDIT:
I feel so stupid , every element dl has the same distance r from the center of rotation... r = a/2 and integral of dl gives AB = a,

therefore
e1 = μI/(4πa) * w * a/2 * a = μI/(4π) * w * a/2 = μI*w*a/(8π)
e = 2*e1 = (μI*w*a)/(4π) obviously wrong approach.

image[/PLAIN] url
uploading pictures