What Is the Maximum Range of a Projectile on an Inclined Plane?

[hadroneater]

Homework Statement

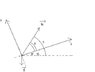
A projectile is launched 80m/s into the air at angle x to the horizontal off the top edge of an infinitely long hill(inclined plane). The hill makes a 35 degrees angle to the horizontal
a) Derive an equation for the range(maximum horizontal displacement).
b) At what angle will the projectile have maximum range?

Homework Equations

I know the equation for range of an even surface and how to derive it but I don't think that will be of help here.

The Attempt at a Solution

Is this question even possible?
I'm tried to derive an equation but with no luck. That's the hard part. I think I just need to differentiate the equation to get the angle of maximum range.

 

[LowlyPion]

You can start with the usual equations and the components of the initial velocity in θ.

The slope adds the additional relationship between the x and y as in

y/x = tan35

 

[Ilivian]

U have several way to approach this question.

1)U may establish the equation representing the way the projectile moving. Establish the equation of the hill. Find the cross point.

2)(I recommend) U consider the line representing the hill the x axis(picture). Do some math and find the result.

Consider the projectile moves along x and y-axis separately:

x axis: x=Vo.cosa.t - (sin35.g.t^2)/2 (1)
y axis: y=Vo.sina.t - (cos35.g.t^2)/2 (2)

When the projectile touch the hill, y = 0
So t=0 (starting point) or t= 2.Vo.sina/(cos35.g) (the time it falls)

Replace t= 2.Vo.sina/(cos35.g) in the equation (1), and u will find the range along the hill (pretty complicated).

To convert the range along the hill to the horizontal range, just multiply the x with cos35.

Now u get the result, try to find at which angle the range is max.

Hard question it is, but do it carefully and u can solve it. Be happy :D