What is the method for finding the centers of circles in the Apollonian Packing?

[CornMuffin]

The Apollonian Packing is generated by starting out with 3 mutually tangent circle and then using descartes theorem to find two other circles that are mutually tangent to each other. This creates 6 curvilinear triangles, and in each, we inscribe a circle tangent to all three of the sides that formed the curvilinear triangle. And we do this for each of the newly formed curvilinear triangles, so the Apollonian Packing looks like this:

Descartes circle theorem states: Given four circles with mutual extermal contact with curvature k_1,k_2,k_3,k_4, then

(k_1+k_2+k_3+k_4)^2=2(k_1^2+k_2^2+k_3^2+k_4^2)

And here is an example

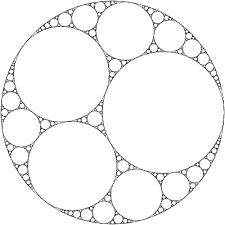
But the one problem that I am having is how do I calculate the center of any of the circles in the Apollonian Packing of Circles

 

[Gevalt]

There is only one point where one circle touches or "kisses" one other circle.
At that point, first, draw the tangent line to the two circles, with the tangent line passing through the kissing point.
Next, draw the perpendicular to the tangent, with the perpendicular also passing through the kissing point.
Each perpendicular will pass through the centres of the two kissing circles.
If you draw all the perpendiculars, their points of intersection will be the centres of the circles.