What is the minimum voltage required to get characteristic spectrum

[Samar A]

Hi,
The x-ray consists of the bremsstrahlung spectrum and the characteristic spectrum. We can get x-rays by using Coolidge tube where there are an applied voltage on the tube between the filament and the target. The bremsstrahlung is depeding on the PD between the filament and the target, but it is produced anyways. The characteristic spectrum requires a high PD to be produced.
I wonder how could we determine the less voltage is sufficient for the emergence of characteristic spectrum by using a diagram of the two spectra, like this:

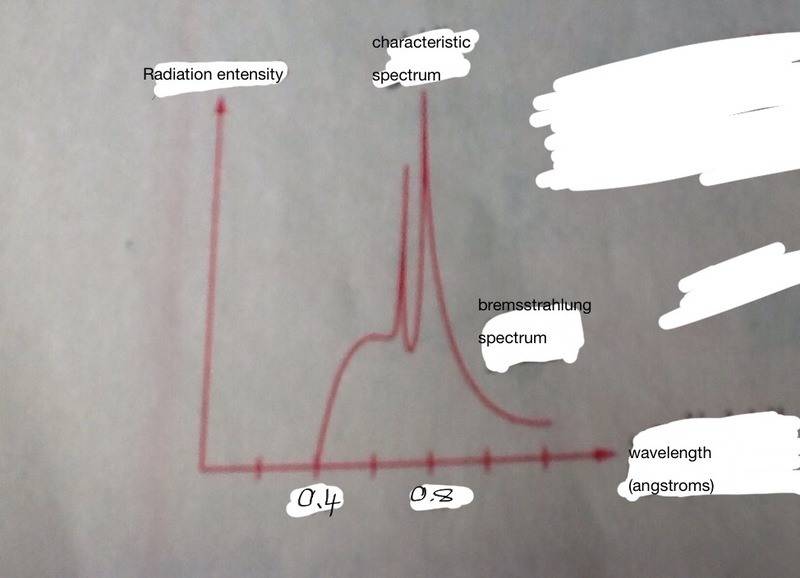
(Note: the information on the photo were not clear so I deleted them and wrote them again using my cellphone)
Anyways, in my textbook it tried to give the less voltage needed for the characteristic spectrum, and it did this:
E=hc/λ =(6.625*10^-34)*(3*10^8)/ (0.8*10^-10)
=2.48*10^-15 J
And then, because E=eV:
2.48*10^-15= (1.6*10^-19) *V
So, V= 1.55*10^4 Volts.

I am not convinced with the way it used and I don't know how to determine it myself, either.
Could someone explain me way it used the value (0.8*10^-10) in the first part of the solution, because I don't think it is the longest wavelength the characteristic would appear.

 

[mfb]

because I don't think it is the longest wavelength the characteristic would appear.

Why not? Characteristic radiation occurs as soon as the total energy of the electrons hitting the cathode is sufficient to excite the atoms in it. You can determine this energy based on the wavelength the atoms emit.

 

[MSDarwish]

Isn't this "Elemtehan"? xD
I'm really happy to see another student in Egypt wants to study correctly
Ok... I know that it's an old topic and you no longer need it, but I think I can help. After googling it for a long time, I've found that you (and I) are right. It shouldn't be calculated this way. 0.08nm doesn't indicate anything to be used as characteristic spectrum wavelength. It's 0.06323nm and 0.07101nm. Also, even if it were the correct wavelength, the calculated energy would be the difference in energy between M and K and between L and K. The required voltage should be the ionization energy of K (as it is required to eject an existing electron and get another into its place to emit an X-ray photon)
I wish it helps.