What is the moment of inertia of the plate about z axis?

[zorro]

Homework Statement

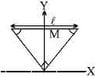
What is the moment of inertia of the plate about z axis?

Homework Equations

The Attempt at a Solution

Consider the isosceles triangle to be a part of a square of side l/root(2)
Its mass will be 2M
We know that its moment of inertia about the centre perpendicular to the plane is 2M(l^2/2)/6=Ml^2/6
Applying parallel axes theorem, moment of inertia about z axis will be Ml^2/6 + 2M(l^2/4)
which is 2/3 (Ml^2)
Moment of inertia of the triangle will be half of it i.e. Ml^2/3
but the answer is Ml^2/6
Please explain if there is any other easier approach.
So the moment of inertia of the triangle will be half of it i.e. Ml^2/12

 

[rl.bhat]

What is the moment of inertia of the plate about z axis?

What is the shape of the plate and the point of suspension?

 

[zorro]

I am sorry I did not post the full question. Here it is.

The figure shows an isosceles triangular plate of mass M and base L. The angle at the apex is 90°. The apex lies at the origin and the base is parallel to X-axis

 

[ehild]

The moment of inertia of the triangle is not half that of the square. See the picture: the points of the upper triangle are farther than those of the lower triangle.

It is easy to get the moment of inertia by integrating (x^2+y^2)dm for the triangle.

ehild

 

[zorro]

The base of the triangle is fixed ( it is of length l). Since the apex angle is 90 degrees and it is isosceles, You get a square when it is rotated about l. So there is no chance of upper triangle being bigger or smaller.

 

[ehild]

How is the moment of inertia defined for an extended body?

ehild

 

[zorro]

here the extended body is a square. So its moment of inertia is same as that of a square.

 

[ehild]

You did not understand me. Forget for the moment that this triangle is half of a square. It is just a set of elementary masses, organized in a certain shape. How would you get the moment of inertia of a set of point masses?

ehild

 

[zorro]

By using the equation ∫x^2 dm

 

[ehild]

What do you mean on x? If x is the horizontal axis, a rod along the y-axis has zero moment of inertia?



ehild