[CODE lang="python" title="Colliding_Ball"]from math import sqrt, atan2, sin, cos, pi, inf
from numpy import array
W = 600 # width of the table
H = 300 # height of the table
R = 10 # the radius of the ball
A = 0 # deceleration constant
dt = 10 ** -3
ma = mb = 1 # masses of the particles a and bdef vec_magnitude(V1):
return sqrt(V1[0]**2 + V1[1]**2)def collision_test(V1, V2):
if vec_magnitude(V1 - V2) <= 2 * R:
return Truedef dot_product(V1, V2):
return sum(V1 * V2)def after_collision_velocity(Va, Vb, Ra, Rb):
''' the equation that produces the velocity of the objects after the collision'''
Va_new = Va - ((2 * mb * dot_product(Va - Vb, Ra - Rb)) /
((ma + mb) * (vec_magnitude(Ra - Rb))**2) * (Ra - Rb))
Vb_new = Vb - ((2 * ma * dot_product(Vb - Va, Rb - Ra)) /
((ma + mb) * (vec_magnitude(Rb - Ra))**2) * (Rb - Ra))
return Va_new, Vb_newdef check_reflection(P, V_mag, angle, V):
if P[1] < R:
P += array([0, 2 * (R - P[1])])
angle *= -1
return P, V_mag, angle, V
if P[0] < R:
P += array([2 * (R - P[0]), 0])
angle = pi - angle
return P, V_mag, angle, V
if P[1] > H - R:
P += array([0, 2 * (H - R - P[1])])
angle *= -1
return P, V_mag, angle, V
if P[0] > W - R:
P += array([2 * (W - R - P[0]), 0])
angle = pi - angle
return P, V_mag, angle, V
else:
V_mag -= A * dt
Vx = V_mag * cos(angle)
Vy = V_mag * sin(angle)
P += array([Vx * dt, 0])
P += array([0, Vy * dt])
V = array([Vx, Vy])
return P, V_mag, angle, Vfile = open("test_drawing.txt", "w")
for line in open("tex.txt", "r"):
t = 0
Xa, Ya, Xb, Yb, Vxa, Vya, Vxb, Vyb = [
int(i) for i in (line.rstrip()).split(" ")]
Pa = array([Xa, Ya], dtype=float)
Pb = array([Xb, Yb], dtype=float)
Va = array([Vxa, Vya], dtype=float)
Vb = array([Vxb, Vyb], dtype=float)
Va_mag = vec_magnitude(Va)
Vb_mag = vec_magnitude(Vb)
if Vxa == 0:
Vxa = inf
angle_a = atan2(Vya, Vxa)
if Vxb == 0:
Vxb = inf
angle_b = atan2(Vyb, Vxb)
while t <= 10:
Pa, Va_mag, angle_a, Va = check_reflection(Pa, Va_mag, angle_a, Va)
Pb, Vb_mag, angle_b, Vb = check_reflection(Pb, Vb_mag, angle_b, Vb)
if collision_test(Pa, Pb) == True:
Va, Vb = after_collision_velocity(Va, Vb, Pa, Pb)
Va_mag = vec_magnitude(Va)
Vb_mag = vec_magnitude(Vb)
if Va[0] == 0:
Va[0] = inf
angla_a = atan2(Va[1], Va[0])
if Vb[0] == 0:
Vb[0] = inf
angle_b = atan2(Vb[1], Vb[0])
t += dt
file.write(str(Pa[0]) + " " + str(Pa[1]) + " " + str(Pb[0]) + " " + str(Pb[1]) + "\n")
print(Pa[0], Pa[1], Pb[0], Pb[1])
file.close()
[/CODE]
[CODE title="data for a simple collision program"]100 200 140 200 4 4 -4 4[/CODE]
[CODE lang="python" title="Drawing Program"]from pylab import plot, show
Xa = [100]
Ya = [200]
Xb = [140]
Yb = [200]
for line in open("test_drawing.txt", "r"):
data = [float(i) for i in line.split(" ")]
Xa.append(data[0])
Ya.append(data[1])
Xb.append(data[2])
Yb.append(data[3])
plot(Xa, Ya, "-r")
plot(Xb, Yb, "-.g")
show()
[/CODE]
Now when you run this you ll get a data of points for each coordinate (Pa, Pb).
The image is like this
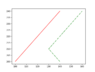
Its clear that ball b reflects but ball a does not. Thats really strange... I mean ball b acts like normal but not the a..
Who can spot the error


, cause I cannot.
P is the position vector so Pa and Pb are the position vectors of the ball
a and ball
b respectively. V is the velocity.

