Jason123
- 3
- 0
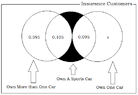
Need help with a probability problem. I have the answer from the answer key, I just don't know how to figure it out.An insurance company examines its pool of auto insurance customers and gathers the following information:1) All customers insure at least one car.
2) 70% of the customers insure more than one car.
3) 20% of customers insure a sports car.
4) Of those customers who insure more than one car, 15% insure a sports car.
Calculate the probability that a randomly selected customer insures exactly one car and that car is not a sports car.
2) 70% of the customers insure more than one car.
3) 20% of customers insure a sports car.
4) Of those customers who insure more than one car, 15% insure a sports car.
Calculate the probability that a randomly selected customer insures exactly one car and that car is not a sports car.