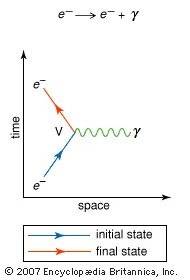
Discussion Overview
The discussion revolves around the calculation of the probability of an electron emitting a photon, particularly through the use of Feynman diagrams. Participants explore the steps required to convert algebraic representations derived from these diagrams into numerical probability values, while addressing the complexities involved in such calculations.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses a desire to understand how to derive a numerical probability from Feynman diagrams but notes a lack of resources that provide concrete final numbers.
- Another participant suggests that while decay widths and cross sections are related to probabilities, detailed numerical results are often left as exercises in textbooks.
- It is mentioned that a specific textbook provides a numerical result (70 pico barns) related to Feynman diagrams.
- One participant claims that the probability of a specific diagram is zero due to conservation laws not being satisfied, emphasizing the need for careful consideration in calculations.
- Another participant highlights that Feynman diagrams represent leading terms in an infinite series and do not directly yield probabilities without further context.
- Questions arise regarding the constants used in calculations, such as the fine structure constant (1/137) and the values related to momentum and energy.
- Clarifications are provided about the importance of using correct units in calculations, particularly regarding the dimensions of physical constants.
- Discussion includes the relationship between the scattering cross section and the momentum of incoming particles, with inquiries about other factors that may influence interaction rates.
- One participant warns against relying on intuition without a solid understanding of prerequisites, suggesting that this approach complicates the learning process for others.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the methods for calculating probabilities from Feynman diagrams, and multiple competing views regarding the interpretation and application of these diagrams remain evident throughout the discussion.
Contextual Notes
Participants note the complexities involved in calculations, including the need for conservation laws, the role of infinite series in Feynman diagrams, and the importance of understanding underlying principles before attempting to derive numerical results.