What is the radius of the circle inscribing a hexagon?

[anemone]

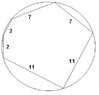
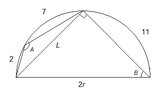
A hexagon with consecutive sides of lengths 2, 2, 7, 7, 11 and 11 is inscribed in a circle.

View attachment 946

Find the radius of the circle.

 

[M R]

solve asin(1/r)+asin(7/(2r))+asin(11/(2r))=pi/2 - Wolfram|Alpha

Does that count as a solution? (Tongueout)

Is Wolframalpha making us lazy?

 

[Farmtalk]

I may be incorrect on this, so please correct me if I am. I have been trying to do a lot of math problems this summer to become better, and I have recently learned since coming back here that I am definitely not as good as I thought I was!:D

Anyway, so I see that two sides of the hexagon are each 11 in length, so if I draw a line from where each of these points connect to the circle, then I have a triangle. And since each side is length 11 each, I can assume it's a 45-45-90 triangle. So then I can use pythagorean's theorem to find the hypotenuse of that triangle, then divide it by two to find the radius:

$$a^2 + b^2 = c^2$$

$$11^2 + 11^2 = c^2$$

$$121+ 121= c^2$$

$$242= c^2$$

$$\sqrt{242}$$ =c

$$\frac{\sqrt{242}}{2} =$$ radius

$$7.778174593052$$ =approximate decimal notation solution of radius

Am I on the right track?

 

[M R]

...I can assume it's a 45-45-90 triangle...

Can you? ;)

 

[Farmtalk]

Can you? ;)

Good point, I probably could NOT. Thanks for that! I'm still pretty new to doing this. I've got a lot of polishing to do!(Blush)

 

[anemone]

solve asin(1/r)+asin(7/(2r))+asin(11/(2r))=pi/2 - Wolfram|Alpha

Does that count as a solution? (Tongueout)

Is Wolframalpha making us lazy?

Hi M R,:)

If you don't mind me asking, could you please tell me more about how exactly did you come up with that brilliant formula? It might be obvious to you but it isn't to me...

Thanks!

And I'm really sorry, your solution isn't complete but the answer is correct though! Good job, Wolfram|Alpha!

 

[chisigma]

Applying the law of cosines You arrive to the equation...

$$\cos ^{-1} (1-\frac{2}{r^{2}}) + \cos^{-1} (1-\frac{49}{2\ r^{2}}) + \cos^{-1} (1-\frac{121}{2\ r^{2}}) = \pi\ (1)$$

... and its solution is $r=7$...

Kind regards

$\chi$ $\sigma$
,

 

[MarkFL]

I began the same way chisigma did, and I noticed this allows the construction:

View attachment 947

The law of cosines gives us:

$$L^2=53-28\cos(A)=4r^2+121-44r\cos(B)$$

Because $A$ and $B$ are opposite angles in a cyclic quadrilateral, we know they are supplementary, and using the identity $$\cos(\pi-x)=-\cos(x)$$, we may write:

$$L^2=53-28\cos(A)=4r^2+121+44r\cos(A)$$

This gives us:

$$\cos(A)=\frac{53-L^2}{28}=\frac{L^2-4r^2-121}{44r}$$

Now, by Pythagoras, we have:

$$L^2=4r^2-121$$

Hence, we may state (after some simplification):

$$\frac{2r^2-87}{7}=\frac{11}{r}$$

Cross-multiplying, we get the cubic:

$$2r^3-87r-77=0$$

This may be factored as:

$$(r-7)\left(2r^2+14r+11 \right)=0$$

Discarding the negative roots, we are left with:

$$r=7$$

 

[Farmtalk]

So what exactly lead you to use the law of cosines for this problem?

 

[MarkFL]

So what exactly lead you to use the law of cosines for this problem?

The law of cosines gives us a convenient way to relate the three sides and one of the interior angles of any triangle.

Also, knowing that $A$ and $B$ are supplementary, and the fact that we also have a right triangle in there helps too. :D